d라이브러리

한 입 베어 물면 바삭한 식감과 고소한 기름, 짭조름한 맛이 입맛을 돋우고, 취향에 따라 달콤한 맛, 매운맛 등 다양하게 즐길 수 있는 치킨! 그래서 모임이나 파티에 빠지지 않는 단골손님이다. 그런데 사람이 많으면 치킨을 몇 마리 시켜야 할지 고민될 때가 있다. 

한 사람당 반 마리 정도 먹는다고 생각하고 시킬지, 다른 야식과 함께 먹을 거니 조금만 시킬지, 남으면 내일 먹어도 되니 넉넉하게 시킬지 등 여러 안이 떠올라 주문하기 전에 망설이게 된다. 

의견을 구하고자 인터넷을 찾아보니 정체를 알 수 없는 서울대학교 학생이 이 문제를 명쾌하게 풀어 놓았다. 바로 ‘피보나치 수열’을 이용하는 것. 피보나치 수열은 1과 1로 시작하고, 앞의 두 수의 합이 바로 뒤의 수가 되는 수열이다. 각각의 수를 ‘피보나치 수’라고 한다. 

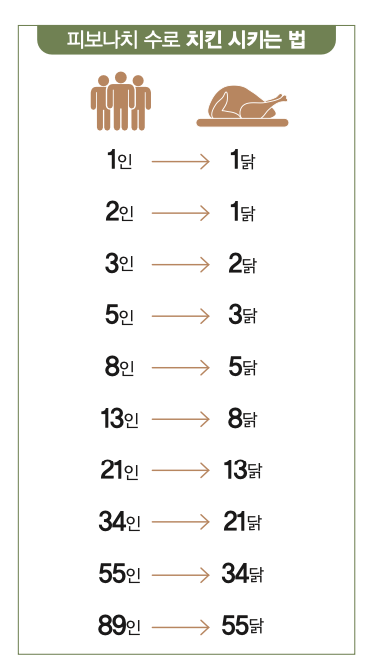
서울대 학생의 방법은 피보나치 수를 사람 수라고 가정하고, 정해진 사람 수의 바로 이전에 있는 피보나치 수대로 치킨을 주문하라는 것이다. 즉 1인이면 치킨 1마리, 2인이어도 1마리, 3이면 2마리, 5이면 3마리 이렇게 말이다.

그런데 이 경우 문제가 있다. 모인 사람 수가 4명, 6명, 7명, 9명, 10명일 때는 답이 없다는 것. 즉 피보나치 수열에는 없는 자연수가 많다. 다행히 서울대 학생은 이 경우에도 해답을 제시했다. 이름도 낯선 ‘제켄도르프 정리’를 이용해 피보나치 수로 분해해 시키라는 것이다. 제켄도르프 정리는 모든 자연수는 하나 이상의 연속하지 않는 피보나치 수의 합으로 나타낼 수 있고, 이는 유일하다는 것이다. 이름은 벨기에의 의사이자 아마추어 수학자 에두아르 제켄도르프에서 유래했다. 제켄도르프는 관련 연구를  1972년 논문으로 발표했지만, 최초의 연구자는 아니다. 20년 전 네덜란드 수학자 헤릿 레케르케르커르가 동일한 연구를 먼저 발표했다. 

예를 들어 100을 피보나치 수로 분해하면 100 = 89 + 8 + 3, 100 = 89 + 8 + 2 + 1, 100 = 55 + 34 + 8 + 3이다. 하지만 이 중 100 = 89 + 8 + 3만 제켄도르프 정리를 따른다. 100 = 89 + 8 + 2 + 1은 1과 2가 연속하는 피보나치 수고, 100 = 55 + 34 + 8 + 3은 34와 55가 연속하는 피보나치 수이기 때문이다. 따라서 100명일 때는 89 + 8 + 3으로 분해되니 89명일 때 55마리, 8명일 때 5마리, 3명일 때 2마리를 합쳐 62마리를 시키라는 것이다. 

치킨 주문마저도 수학적으로 생각하다니 수학의 매력은 참으로 끝이 없다.