d라이브러리

수학자의 호기심은 끝이 어딜까? 피자를 공평하게 나눠 먹는 기상천외한 방법은 수학자의 단골 연구 주제다. 

피자를 자를 때 모든 선이 원의 중심을 지나도록 한다면 똑같이 나누기가 비교적 쉽다. 하지만 선들이 원의 중심이 아닌 다른 점을 중심으로 지난다면 어떨까? 조각마다 크기가 다르니, 조각을 고를 때마다 신중할 수밖에 없다. 둘이서 남아 있는 조각 중 가장 큰 조각과 작은 조각을 한 세트로 번갈아 골라 먹는다 해도 조각을 고르는 순서를 어떻게 정할지도 문제고, 다 먹은 다음 서로 먹은 총량이 같을지도 장담할 수 없다. 

수학자 릭 마브리와 폴 다이어만은 피자를 자를 때 그은 선의 개수에 주목해 연구했다. 피자 대신 종이에 커다란 원을 그리고 원의 중심이 아닌 다른 점(아래쪽 그림 참고)을 중심으로 선을 그었다. 그리고 각 도형들을 흰색, 연두색, 흰색, 연두색으로 번갈아 색칠했다. 

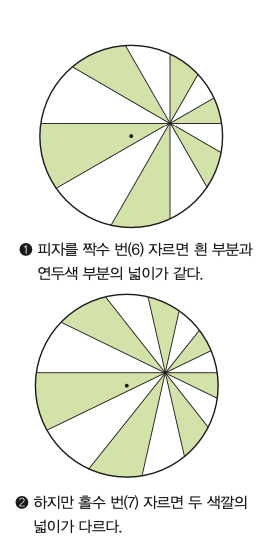
연구 결과 피자를 4번 이상의 짝수로 자르면 흰색 부분과 연두색 부분의 총량이 같다는 것을 발견했다. 하지만 4번 이상의 홀수로 자르면 원의 중심이 들어 있는 색깔 부분의 총량이 훨씬 많았다. 예를 들어 피자를 7번 잘랐는데, 원의 중심이 연두색 부분에 들어 있다면 연두색 부분의 피자 총량이 흰색 부분의 피자 총량보다 많았다.

피자를 3회 이하로 자르면 선들이 원의 중심을 지나는 경우에만 총량이 같았다. 만약 선들이 원의 중심을 지나지 않는다면, 원의 중심이 들어 있는 색깔의 총량이 훨씬 많았다. 

두 수학자는 원의 중심을 지나도록 선을 긋거나 짝수 번 자르면 서로 마주 보는 조각끼리 대칭을 이뤄 넓이가 같아진다고 설명했다. 자르는 선이 원의 중심을 지나지 않거나 홀수 번 자르면 선의 개수 같은 조건에 따라 크기가 어떻게 달라지는지를 여러 가지 수학식으로 나타내 알아봤다.  

그러니까 상대방보다 내가 피자를 더 많이 먹으려면 선을 몇 번 그어 피자를 잘랐는지 센 다음, 원의 중심이 어디에 속하는지 확인해야 한다. 피자 한 번 더 많이 먹기 어렵다. 이 모든 걸 감수할 만큼 피자가 맛있어야 시도할 만한 방법이다.

칼질을 4번만 해서 공평하게 나눠 먹으려면? 

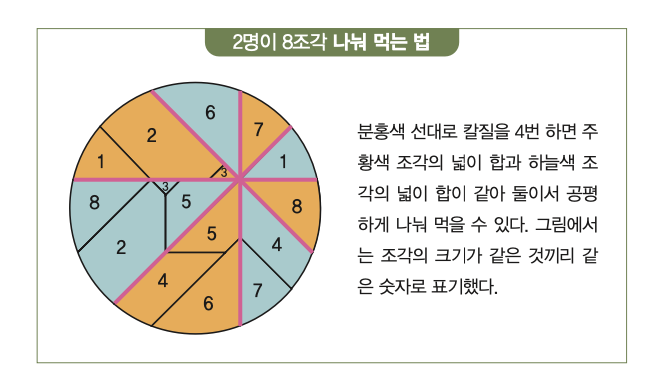
이번에는 칼질을 4번만 할 수 있다. 즉 피자 가운데가 아닌 아무 곳이나 기준점을 잡고 4번 칼질해 크기가 서로 다른 8조각을 만들었을 때 두 사람이 공평하게 나눠 먹는 방법이다. 

1967년 미국수학협회에서 발행하는 <;수학 잡지>;에 나온 이 문제는 1994년이 돼서야 해결책이 나온다. 정답은 어디를 중심으로 잡든 360를 8등분한 45로 유지되게 칼질을 4번 한 뒤 아무 조각이든 하나를 고른 뒤, 시계 방향이든 반시계방향이든 연달아 있는 조각을 차례로 하나씩 골라 먹으면 된다. 

1994년 수학자 래리 카터와 스탠 웨이건은 직소 퍼즐처럼 피자를 조각내는 ‘해체 퍼즐’ 방법으로 수식 없이 이 문제를 증명했다. 해체 퍼즐은 같은 조각으로 서로 다른 기하학적 형태를 만드는 퍼즐이다. 두 사람은 8조각을 각각 더 작은 조각으로 나눈 뒤 똑같은 모양으로 2개씩 짝지어 해결했다.

2012년 수학자 그렉 프레드 릭슨은 8보다 크거나 같으며, 4로 나뉘는 모든 수에 대해 이 문제를 풀 수 있다는 것을 증명한다. 일명 ‘피자 정리’! 중심을 어느 곳으로 잡든 일정한 각도로 자르면 n명이 4n 조각을 똑같은 양으로 나눠 먹을 수 있다는 것이다.