당연하다고 생각한 소시지 모양에도 수학이 숨겨져 있다. 알사탕 여러 개를 포장할 때 어떤 구조로 포장하면 가장 작은 부피가 나올까? 1975년 헝가리 수학자 페예시 토트 라슬로는 5차원 이상에서는 구의 수에 상관없이 가장 작은 부피를 가지는 압축 포장 방법은 소시지 모양으로 길쭉하게 포장하는 것이라고 추측했다. 일명 ‘소시지 추측’이다. 이후 수학자들은 5차원 이상은 물론 2~4차원에서는 어떤 모양으로 포장해야 최소 부피(혹은 넓이)가 되는지 알아봤다.
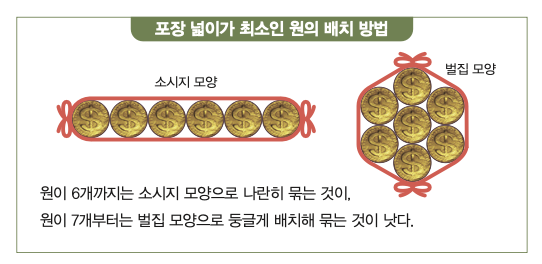
먼저 2차원 평면에서 같은 크기의 원이 여러 개 있을 때 이 원들을 가장 짧은 끈으로 포장하는 방법은 무엇일까? 떠올리기 쉽게 동전 초콜릿을 생각하자. 이때 부피는 무시한다. 6개까지는 소시지 모양으로 길게 한 줄로 세우는 것이 가장 작은 면적을 갖고, 7개부터는 벌집 모양으로 둥글게 뭉쳐 배치하는 게 가장 작은 면적을 갖는다. 100개, 1000개로 늘어나도 이 답은 변하지 않는다.
그렇다면 3차원 구는 어떨까? 3차원에서도 2차원과 마찬가지로 어느 정도까지는 소시지 모양으로 나열하는 것이 좋고, 특정 개수 이상부터는 빽빽하게 벌집 모양으로 뭉쳐 놓는 것이 좋다. 3차원에서 소시지 모양 포장의 경계는 56개다. 즉 구의 개수가 56개 이하일 때는 소시지 모양으로 포장하는 것이 좋고, 57개부터는 중심을 기준으로 빽빽하게 뭉쳐서 포장하는 것이 좋다.
문제는 4차원에서부터다. 2, 3차원까지는 어떻게든 상상도 되고 복잡해도 계산해볼 만했지만 4차원, 5차원, 6차원으로 쭉쭉 나아가면 구가 어떻게 생겼을지 그려지지도 않고 계산은 더더욱 힘들어진다. 수학자에게도 이 문제는 쉽지 않았다. 페예시 토트의 추측처럼 정말 소시지 모양이 항상 나을지 증명하는 것은 오랜 시간 난제로 남아 있었다.
4차원의 경우, 구가 5만 개 이하일 때는 소시지 모양으로 포장하는 것이 최소 부피라는 것이 밝혀졌다. 하지만 10만 개가 넘어가면 벌집 모양으로 배열하는 것이 나았다. 그렇다면 4차원의 경계는 얼마일까?
그건 아직 밝혀지지 않았다. 4차원에서는 5만 개와 10만 개 사이 어딘가에 소시지 모양과 벌집 모양의 경계가 있다는 사실만 알 뿐이다.
5차원부터는 그 내용이 조금 다르다. 만약 페예시 토트의 소시지 추측이 사실이라면 5차원 이상일 때는 차원마다 소시지 모양과 벌집 모양을 나눠 계산할 필요도 없고, 거기에 사는 사람은 언제든 고민 없이 소시지 모양으로 선물을 포장하면 된다. 과연 이 추측은 사실일까?
1998년 독일 수학자 울리히 베트케와 마틴 헨크, 외크르 월스는 소시지 추측에 힘을 싣는 연구 결과를 발표한다. 42차원 이상에서는 항상 소시지 모양 포장법이 최소 부피를 차지한다는 사실을 증명한 것이다. 하지만 5차원~41차원에서는 아직 어떤 구조로 구를 포장해야 가장 부피가 작은지 밝혀지지 않았다.












