d라이브러리 2024년 01월 수학동아

6조각, 9조각, 20조각 맥너겟 수

맥도날드에서 파는 맥너겟이 이름에 들어가는 수가 있다. 처음 들어봤다면 대체 어떤 수인지 짐작도 안 갈 텐데, 놀랍게도 수학계 오래된 문제와 관련있다.

1980년대 영국 맥도날드에서는 맥너겟을 6조각, 9조각, 20조각씩만 상자에 담아 팔았다. 이를 본 수학교육자 앙리 피치오토는 그 자리에서 한 수학 문제를 떠올렸고 냅킨에 풀이를 적었다. 바로 ‘동전 문제’다. 맥너겟 수는 이 문제의 한 예시다.

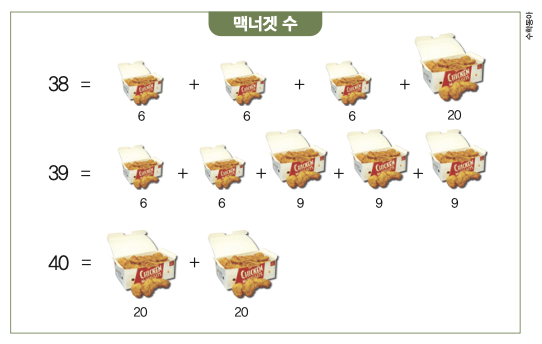
먼저 맥너겟 수부터 알아보자. 6, 9, 20은 공약수가 1뿐인 서로소기 때문에충분히 큰 어떤 수는 이 세 수의 결합으로 나타낼 수 있다. 즉 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, 43을 제외한 모든 자연수는 맥너겟 상자 조합으로 만들 수 있다. 이 수를 맥너겟 수라고 한다. 맥너겟 수에 맥너겟 수를 더하거나 곱해도 맥너겟 수다.

그렇다면 맥너겟 수가 어떻게 동전 문제와 연결되는 걸까? 맥너겟 수가 아닌 가장 큰 자연수 43이 서로소인 세 수 6, 9, 20의 동전 수기 때문이다. 동전 문제는 서로 다른 동전이 있을 때 이 동전으로 만들 수 없는 가장 큰 수를 찾는 문제다. 19세기 독일 수학자 페르디난트 프로베니우스가 강의 도중 이 문제를 자주 소개해서 그의 이름을 따서 ‘프로베니우스 문제’라고도 부른다.

예를 들어 2원짜리 동전과 5원짜리 동전이 있다면, 두 동전의 조합으로 만들 수 없는 금액은 1원과 3원뿐이다. 그 외의 금액은 모두 만들 수 있다. 이때 두 동전으로 만들 수 없는 가장 큰 수인 3이 동전 수이고, 이를 찾는 문제가 바로 동전 문제다.

1882년 영국 수학자 제임스 실베스터는 서로소 관계인 두 수가 있을 때 동전 수를 찾는 방법을 공식으로 만들었다. 그 이유는 서로소인 수 사이에서만 동전 수가 있기 때문이다. 서로소인 두 수 a와 b의 동전 수는 (a - 1)(b - 1)-1이다.

▼이어지는 기사를 보려면?

Part1. 군침 자극~ 맛있는 수학

Part2. 푸딩 쏙 빼닮은 블랑망제 함수

Part3. 포장의 달인 소시지 추측

Part4. 군침 돌고 맛있게 계량 수학

Part5. 살살 녹는 고기의 비밀은 방정식으로

Part6. 수학자의 레시피, 그 맛은?

Part7. 피자 먹을 때 나도 모르게 수학한다! 빼어난 정리

Part8. 피자를 공평하게 먹는 방법! 피자 정리

Part9. 불만 없이 케이크 나누기 고독한 분할법