d라이브러리

난 매우 고집이 센 수학자였어. 늙으면 고집이 세진다고 하지만 난 젊어서부터 내 주장을 쉽게 굽히지 않았지. 그래서인지 내 주변엔 친구나 함께 연구하려는 사람이 없었네.
 

 
내가 택한 길이지만 외로웠던 건 사실이야. 이제 와 드는 생각이지만 다른 사람의 이야기도 듣고 많은 연구를 함께할 수 있었다면 좋았을 텐데…. 난 이미 고집 센 늙은이로 생을 마감해 버렸지. 허허. 하지만 그 고집 때문에 프랙탈을 발견할 수 있었는지도 몰라.

IBM에서 일하던 어느 날, 영국의 수학 천재 루이스 리처드슨이 1961년에 발표한 논문을 읽다가 나는 아르키메데스처럼 “유레카”를 외쳤네. 발가벗고 목욕탕을 뛰쳐나갈 뻔했다니까. 논문은 영국의 해안선 길이가 측정하는 자의 눈금이 작을수록 길어진다는 내용이었어. 다른 수학자들은 이 논문에 별 관심이 없었지만, 나는 해안선을 자세히 들여다보면 해안선도 같은 모양이 무한히 반복되는 프랙탈 구조라는 사실을 알게 됐지. 그동안 내가 고민했던 잡다한 연구의 결론을 찾게 된 거지.

프랙탈을 발견한 후 나의 연구는 가속도가 붙었다네. 바로 새로운 공간과 차원을 정의했지. 사실 내가 논문을 발표하기 이전에 소수(또는 분수) 차원이 존재한다는 주장이 제시됐네. 독일의 수학자 펠릭스 하우스도르프에 의해서였어. 쉽게 말해 1차원, 2차원 외에 1.4차원과 같은 소수 차원이 존재한다는 것이었지. 하우스도르프 는 이것을 ‘하우스도르프 차원’이라는 이름으로 세상에 알렸어. 하지만 그는 하우스도르프 차원의 존재성을 완벽히 증명하지는 못했어. 수학자들도 이것을 하나의 추측으로만 취급했지. 나는 이 소수 차원을 프랙탈 차원이라 정의하고 증명했어. 이렇게 할 수 있었던 힘은 프랙탈 기하학이 있었기 때문이었으니까. 그래서 나는 1967년 미국의 세계적인 과학저널 ‘사이언스’에 논문을 발표하고, 프랙탈 차원을 세상에 알렸지.
 

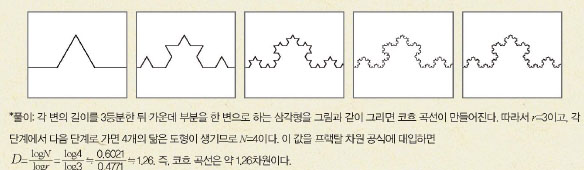
✚칸토어 집합과 코흐 곡선의 차원
 

집합론을 창시한 독일의 수학자 게오르크 칸토어는 ‘칸토어 집합’을 연구했다. 이것은 수학적으로 연구된 최초의 프랙탈 중 하나다. 하지만 안타깝게도 칸토어는 칸토어 집합이 프랙탈이라는 사실을 알지 못했다. 칸토어 집합은 0과 1 사이의 실수로 만들어진 집합이다. 칸토어 집합을 만들려면 오른쪽 그림과 같은 과정을 반복해야 한다.
 

공간과 차원에 대한 연구는 꾸준히 다른 수학자들에 의해 더욱 발전해 다른 학문에도 큰 영향을 미쳤어. 프랙탈 차원의 정의 덕분에 자연 현상에 대한 설명은 물론 과학 분야와 의학 분야 연구에도 활기를 띠게 됐으니까. 예를 들면, 어떤 바이러스에 반응하는 어떤 항체의 경우 바이러스와 항체가 결합하는 부분이 약 2.4차원으로 같아 정확하게 반응한다는 연구결과가 나왔더군. 허허
 

▼관련기사를 계속 보시려면?

프랙탈의 대부 만델브로 이야기 
대학 입학 수학 시험, 그림으로 풀다
고집 센 외톨이 수학자
내 안에 또 다른 나 있다
함께 그려 보는 프랙탈 아트 
수학 배틀! 최강 도시를 가린다
꿈의 대회 창시자는 나! 콘스탄티노프
이런 수학문제 봤나요?
기억 속에 남는 아름다운 수학문제
최강 수학도시는 어딜까?