d라이브러리

<이상한 나라의 앨리스>처럼 몸이 커졌다가 줄어들진 않지만, 개미처럼 작은 사람들이 사는 소인국으로 갔다가 고래를 어깨에 짊어질 만큼 큰 거인들이 사는 세계에 떨어진 사람의 이야기가 있다. 바로 아일랜드 작가 조너선 스위프트의 <걸리버 여행기>다.

 

뱃사람이자 의사인 레뮤엘 걸리버는 항해 도중 거센 폭풍에 휩쓸려 조난을 당한다. 파도에 쓸려 다니다가 어느 순간 땅에 발을 딛지만, 그는 곧 정신을 잃는다. 다시 정신이 들었을 때는 꼼짝도 할 수 없었다. 머리카락부터 발끝까지 땅에 꽁꽁 묶여 있었기 때문이다. 잠시 후 걸리버의 가슴 위로 사람이 올라오는데, 키가 고작 15cm밖에 되지 않았다. 그곳은 소인국이었다. 

 

 

 

걸리버는 소인국 사람들을 도와주면서 릴리퍼트 국왕에게 인정을 받는다. 릴리퍼트의 국왕과 걸리버가 맺은 조약 중에는 ‘릴리퍼트는 걸리버에게 1,728명을 먹일 수 있는 음식을 제공한다’라는 항목이 있다. 왜 1,700이나 1,800이 아니라 딱 떨어지지 않는 숫자인 1,728명일까?

 

신장 측정 결과 걸리버의 키가 릴리퍼트의 사람보다 약 12배 컸기 때문이다. 길이가 12배 커지면 면적은 12의 제곱, 부피는 12의 세제곱만큼 커진다. 간단히 선분과 사각형, 정육면체를 예로 들어보겠다. 

 

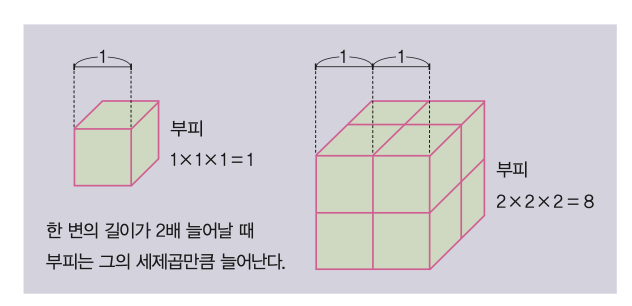
한 변의 길이가 1인 정사각형의 넓이는 1의 제곱인 1, 정육면체의 부피는 1의 세제곱인 1이 된다. 한 변의 길이가 12인 정사각형의 넓이는 12의 제곱인 144, 정육면체의 부피는 12의 세제곱인 1728이 된다.

 

 

 

걸리버의 키가 소인보다 12배 크다고 한 것은 당시 영국에서 12진법을 많이 쓰고 있었기 때문이다. 12진법은 아직 영국에서 쓰는 단위에 흔적이 남아 있다. 예를 들어 1피트(약 30cm)는 12인치(약 2.54cm)다.

 

 

 

소인국을 떠나 무사히 집으로 돌아간 걸리버는 얼마 뒤 다시 배를 타고 여행을 떠난다. 그리곤 거인들이 사는 브로브딩내그에 도착한다. 거인들의 손아귀에 들어갈 정도로 작은 걸리버는 브로브딩내그의 음악 소리가 너무 커서 잘 들을 수 없다고 불평한다. 

 

그런데 과연 거인의 악기에서 나는 소리가 크기만 할까? 악기에서 소리가 나는 이유는 악기가 공기를 진동시키기 때문이다. 이때 1초에 진동하는 횟수를 진동수라고 하는데, 단위로는 헤르츠(Hz)를 사용한다. 진동수가 클수록 높은음이 나고 작을수록 낮은음이 난다. 현악기의 경우 진동수와 현의 길이는 반비례 관계다. 현의 길이가 2배 늘어나면 진동수는 1/2이 되고, 현의 길이가 1/2이 되면 진동수는 2배가 된다.

 

이 사실을 바탕으로 브로브딩내그의 악기에서 어떤 소리가 나는지 추측해볼 수 있다. 우리가 사용하는 도레미파솔라시도 음계에서 기본 도의 진동수는 약 260Hz이다. 현의 길이가 2배일 때 도의 진동수는 약 130Hz, 4배일 때는 약 65Hz가 된다.

 

브로브딩내그는 걸리버의 세계보다 모든 것이 약 12배 크기 때문에 악기도 12배 클 것이다. 따라서 브로브딩내그의 악기에서 나오는 도의 진동수는 260/12Hz=21.666…Hz라고 추측할 수 있다. 진동수는 현의 굵기와도 반비례한다. 악기가 커져 현의 굵기가 굵어지면 진동수는 더욱 작아진다.

 

사람이 들을 수 있는 진동수의 범위는 20~20000Hz이므로, 책의 내용과 달리 걸리버는 거인들의 악기에서 나오는 낮은 진동수의 소리를 거의 듣지 못했을 가능성이 크다.

 

실제로 덩치가 큰 동물은 진동수가 낮은 저주파를 이용해 의사소통하기도 한다. 대표적으로 몸길이가 30m에 달하기도 하는 수염고래는 암컷을 유혹하기 위해 사람이 들을 수 없는 낮은음을 내는데, 이 소리는 주파수가 매우 낮아 수천 km 떨어진 곳까지 전달된다. 땅 위에서는 코끼리가 저주파를 이용해 의사소통한다고 알려져 있다.

 

소인국, 거인국을 거쳐 걸리버는 공중 도시 라퓨타로 간다. 그는 집으로 무사히 돌아갈 수 있을까? 어릴 적 본 걸리버 여행기가 기억이 나지 않는다면 <걸리버 여행기>를 읽으면서 수학적 내용까지 살펴보자.