d라이브러리

따라서 ‘도전! 수학자’에서는 수를 그림으로 나타내는 미션을 통해 수학 유망주를 선발하고자 합니다. 그럼 미션을 공개하겠습니다. 칠판에 적힌 그림이 의미하는 바를 맞히세요!
어떻게 답을 찾아야 할지 많이 당황스럽다고요? 그래서 몸 풀기 미션을 준비했습니다. 각자의 휴대전화에 전송된 펑 메시지를 확인하세요!


피보나치 수를 그림으로 나타내라!

당신은 지금부터 이탈리아의 수학자 레오나르도 피보나치입니다. 피보나치가 되어 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …로 이어지는 수의 규칙을 연구하고, 이 수를 그림으로 나타내세요. 이 메시지는 30분이 지나면 ‘펑~!’ 하고 터지는 펑 메시지입니다. 폭탄이 터지면 수학 유망주 선발전에서 바로 탈락하게 되니, 30분 안에 미션을 해결해 주세요!

1과 1, 두 수를 시작으로 앞의 두 수를 더해 만들어지는 피보나치 수는 이탈리아의 상인이자 수학자였던 레오나르도 피보나치가 <;주판서>;라는 책에 소개하면서 유명해졌다. 대대로 상인 집안이었던 피보나치는 12세기 무렵 이슬람인과 무역을 활발히 하고 있었다. 당시 이슬람인은 인도에서 전해진 수 체계를 계산에 편리하도록 변형해 사용하고 있었는데, 피보나치는 이 수의 편리함을 알고 유럽의 많은 사람들에게 소개하기 위해 1202년에 <;주판서>;를 지었다. 이슬람인이 사용한 수는 현재 우리가 사용하고 있는 아라비아 숫자의 모태가 되는 수로, 생김새만 조금 달랐을 뿐 모든 기능은 현재와 똑같았다.

그런데 <;주판서>;의 12장에는 토끼 수의 증가를 예로 피보나치 수가 소개돼 있다. 이 책은 출판 이후 300년가량 큰 인기를 끌었는데, 덕분에 피보나치 수도 유명해졌다. 이후 1, 1, 2, 3, 5, 8, …로 이어지는 수의 나열을 ‘피보나치 수열’이라고 하고, 각각의 수를 피보나치 수라고 불렀다.


피보나치 수는 2×n 타일 채우기

평소 수학 이론을 시각화 하는 데 관심이 많았던 미국의 수학자 로버트 디카우는 1997년 피보나치 수를 그림으로 나타냈다. 그는 색이 다른 두 개의 정사각형 타일을 이어 붙인 뒤, 이 타일을 기준으로 삼았다. 그리고 기준이 되는 타일을 2×(n-1)표에 배열하는 방법의 수를 헤아려 보았다. 여기서 n은 2보다 크거나 같다. 그랬더니 첫 번째 항인 2×1표에서는 타일을 배열하는 경우의 수가 1개, 두 번째 항에서는 2개, 세 번째 항에서는 3개, 네 번째 항에서는 5개로 피보나치 수를 따랐다. 이때 타일을 회전해서 같은 모양이 되는 경우는 모두 같은 것으로 간주하기 때문에 통틀어 1가지로 셌다. 즉, 2×(n-1)표에 타일을 채우는 방법의 수와 피보나치 수가 같음을 이용해 피보나치 수를 그림으로 표현한 것이다.
 
S(5, 4)를 오각형으로 나타내라!

첫 번째 미션을 해결한 여러분은 축하합니다. 두 번째 미션은 스코틀랜드의 수학자 제임스 스털링이 되어 S(5,4)를 오각형으로 나타내는 겁니다. 도통 무슨 소리인지 모르겠다고요? 제1종 스털링 수가 무엇인지 알아보면 감이 오실 겁니다. 이번 미션도 첫 번째 미션과 마찬가지로 30분 안에 풀지 못하면 탈락의 고배를 마시게 됩니다. 그럼 지금부터 시작합니다!

고등학교 경우의 수 문제에서 가장 많이 등장하는 것은 n명의 사람을 둥근 탁자에 앉히는 방법의 수나, n개의 서로 다른 공을 k개의 구별이 없는 상자에 넣는 방법의 수를 묻는 것이다. 각각 ‘제1종 스털링 수’와 ‘제2종 스털링 수’라고 불리는 이 수는 18세기 스코틀랜드의 수학자 제임스 스털링이 처음 소개한 수로, 수리 논술 문제의 단골손님이다. 그렇다면 제1종 스털링 수는 어떻게 구할까? 예를 들어 종석, 우빈, 신혜, 보영 이렇게 네 사람이 탁자 2개에 나눠 앉는 방법을 구해 보자. 이때 두 개의 탁자는 똑같은 모양이다.

우선 둘씩 짝지어서 앉는 방법이 있다. 남자는 남자끼리 여자는 여자끼리 나눠 앉을 수 있고, 반대로 남녀가 짝을 이뤄 앉을 수 있다. 이 경우를 일일 따져 보면 전자가 1가지, 후자가 2가지로 총 3가지다.

세 명이 함께 앉고 혼자 앉는 경우도 따져야 한다. 그런데 이때에는 세 명이 탁자에 어떻게 앉는지를 주의 깊게 살펴봐야 한다. 시계방향 순으로 종석과 우빈, 신혜가 앉는 것과 종석과 신혜, 우빈이 앉는 것은 서로 다른 경우이기 때문이다.

이점을 고려해 경우의 수를 세면 총 8가지가 된다. 결국 4명이 2개의 둥근 탁자에 앉는 방법의 수는 11가지라는 결론을 얻게 된다. 그런데 수학에서는 이것을 S(4,2)=11이라고 표기한다. 즉 n명을 k개의 둥근 탁자에 앉히는 경우의 수를 S(n,k)라고 나타내는 것이다.
 
제1종 스털링 수는 다각형으로 나타낸다!

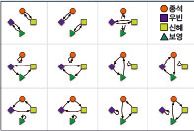
제1종 스털링 수를 어떻게 그림으로 나타낼 수 있을까? 바로 다각형의 각 꼭짓점을 사람이라고 가정하고, 옆에 앉은 사람을 화살표로 표시하는 것이다. 누가 언제부터 이런 방법을 써서 표현했는지는 정확하게 알려지지 않았지만, 수학자들은 오래전부터 이렇게 나타냈다.

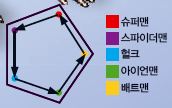
그러면 이제 S(5,k)를 어떻게 오각형으로 나타낼 수 있는지 자세히 알아보자. 예를 들어 슈퍼맨과 스파이더맨, 헐크, 아이언맨, 배트맨 이 다섯 명의 슈퍼히어로가 한 개의 둥근 탁자에 나눠 앉는다고 가정하고 각각의 히어로를 오각형의 꼭짓점으로 표시해 보자. 그런데 꼭짓점 위에 점을 찍으면 오각형과 겹쳐 잘 안 보인다. 따라서 꼭짓점 바로 아래 점을 찍는다. 그리고 오른쪽 바로 옆에 앉은 사람을 화살표로 표시한다. 만약 슈퍼맨의 오른쪽에 스파이더맨이 앉았다면, 슈퍼맨이 스파이더맨을 가리키는 화살표를 그린다. 아이언맨의 오른쪽에 배트맨이 앉았다면, 아이언맨이 배트맨을 가리키는 화살표로 표시한다. 이런 규칙에 따라 그림을 그리면 제1종 스털링 수를 그림으로 나타낼 수가 있다.

주어진 미션 S(5,4)는 슈퍼히어로 다섯 명이 네 개의 둥근 탁자에 앉는 경우의 수다. 사람이 아무도 않지 않는 탁자는 없어야 하기 때문에 탁자마다 적어도 한 명씩은 앉아야 하고, 어느 한 탁자에는 두 명이 앉아야 한다. 따라서 다섯 명 중에서 두 명을 뽑는 경우의 수와 같아진다. 즉 슈퍼맨과 스파이더맨, 슈퍼맨과 헐크, 슈퍼맨과 아이언맨 등 총 10가지 경우의 수가 생긴다. 이를 그림으로 나타내면 아래와 같다.
 
카탈란 수를 서로 다른 4가지 그림으로 나타내라!

어려운 문제까지 잘 해결하셨습니다. 드디어 마지막 몸 풀기 미션입니다. 이 문제만 해결하면 최종 미션에 도전할 수 있으니 끝까지 힘을 내 주세요!
마지막 미션 나갑니다. 벨기에의 수학자 외젠 샤를 카탈란의 연구를 참고해, 카탈란 수를 네 가지 방법으로 시각화 하세요!

카탈란의 연구노트

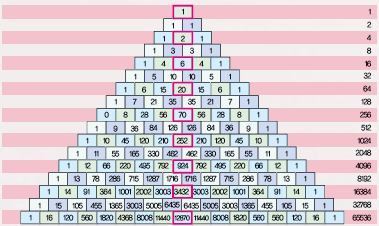
나는 세 개의 기둥에 서로 다른 n개의 원판을 크기 순서대로 꽂는 하노이의 탑을 연구하다 놀라운 수를 발견했다. 바로 1, 1, 2, 5, 14, 42, 132, …순으로 이어지는 수의 나열이다. 이 수가 신기한 것은 파스칼의 삼각형에서 홀수 줄에 위치한 수 중 가장 가운데 있는 수 즉 1, 2, 6, 20, 70, …를 각각 1, 2, 3, 4, 5, …로 나눈 값과 같기 때문이다. 또한 오일러가 연구한 서로 다른 꼭짓점을 이어 (n+2)각형을 n개의 삼각형으로 나누는 경우의 수와도 같다.

나는 카탈란 수가 되는 다른 경우가 더 있는지 궁금했고, 후세 수학자들의 연구를 샅샅이 뒤져 본 결과 66가지나 있다는 걸 알아냈다. 그 중 몇 가지를 소개하면, 각각 n개인 ‘ ’와 ‘ ’로 산을 그리는 방법의 수, 크기가 n인 계단을 직사각형 n개로 분할하는 방법의 수 등이다.

노트의 여백이 모자라 각각의 경우에 해당하는 그림은 생략한다. 누구나 쉽게 그림으로 표현할 수 있으니 도전해 보길 바란다.
 
가지각색 카탈란 수

카탈란의 연구노트에 소개된 여러 가지의 경우를 그림으로 표현해 보자. 조합론에서 카탈란 수는 n에 따라 C$_{n}$으로 표기한다.

➊ n개의 ‘ ’와 ‘ ’로 산을 그리는 방법의 수
산을 그리라고 하면 대부분의 사람들은 삼각형 모양으로 우뚝 솟은 산을 그린다. 여기서도 ‘ ’와 ‘ ’를 이용해 삼각형 모양의 산을 그리면 n에 따른 경우의 수가 카탈란 수가 된다.

➋ n+1개의 나뭇잎을 가지는 이진 수형도
수형도란 나뭇가지 모양의 그래프로, 점과 선으로만 구성되어 있다. 점을 ‘노드’라고 부르는데, 이진 수형도는 한 개의 노드가 최대 두 개의 ‘자식노드’를 가지는 수형도를 뜻한다. 여기서 자식노드란 한 노드에서 뻗어 나와 생긴 노드다. 노드 중 자식노드가 딸리지 않은 노드를 ‘단말노드’라고 부르는데, 카탈란 수가 되는 이진 수형도는 n+1개 단말노드를 가지는 경우의 수다. 여기서는 자식노드는 점, 단말로드는 나뭇잎으로 표시했다.

➌ 크기가 n인 계단을 직사각형 n개로 분할하는 방법의 수
가로·세로의 길이가 n인 계단을 직사각형 n개로 분할하는 경우의 수를 구하면 카탈란 수가 구해진다. 가로·세로 길이가 1인 계단은 그 자체가 직사각형 1개이기 때문에 경우의 수는 1가지다. n이 2일 때는 가로선과 세로선을 이용해 각각 직사각형 2개로 분할할 수 있으므로 2가지가 된다.

별별 수 HOT 3

뜨거운 열기 속에 ‘도전! 수학자’가 진행되고 있습니다. 이제 마지막 관문만 남았는데요, 처음 제시된 최종 미션만 해결하면 됩니다. 정답자가 나오는 대로 시상식이 진행될 예정이니, 자리를 뜨지 마시고 별별 수 HOT3을 만나 보시기 바랍니다.
수학자들은 수를 아름다운 기하학적인 도형으로 표현하기 위해 끊임없이 노력하고 있습니다. 그 결과 다양한 수들이 각양각색의 모양으로 변신했습니다. 그 화려한 자태를 확인해 보세요!

1. 중심 십각 소수

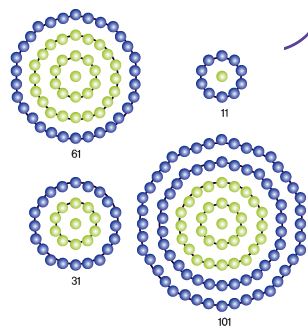
1을 시작으로 10, 20, 30, … 등 10단위로 늘어나는 수, 즉 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, … 중에서 1과 자기 자신으로만 나눠떨어지는 소수를 수학자들은 ‘중심 십각 소수’라고 부른다. 중심 십각 소수는 11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, …순으로 이어지는데, 신기한 것은 11부터 281까지 수는 10단위로 커진다는 것이다.
즉, 11=1+10, 31=1+10+20, 61=1+10+20+30, 101=1 +10+20+30+40, 151=1+10+20+30+40+50, 211=1+ 10+20+30+40+50+60, 281=1+10+20+30+40+50+60+70이다.
수학자들은 이런 특이한 성질을 가진 중심 십각 소수를 마치 진주목걸이처럼 10개 단위로 묶어 그림으로 나타냈다.
 
2. 별 수

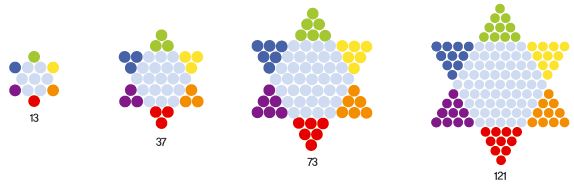
수를 정다각형 말고 다른 방법으로 나타낼 수는 없을까? 수학자들은 피타고라스학파처럼 점을 배열해 예쁜 모양을 만드는 작업에 몰두했고, 결국 별 모양의 수를 만들어냈다. 일명 ‘별 수’라고 불리는 수로, 6n(n-1)+1을 만족하는 수 중 n이 1일 때부터 43번째까지 수를 말한다. 즉 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, …, 순으로 이어져 10333, 10837에서 끝나는 수다. 두 번째 별 수부터는 정삼각형 모양으로 배열된 점과, 정육각형 모양으로 배열된 점들이 조화롭게 구성되어 별 모양을 이룬다. 자칫 삼각수와 육각수를 더한 것으로 착각할 수 있는데, 삼각수나 육각수 안에 점을 더 채워 넣은 모양으로, 삼각수나 육각수가 아니다.
 
3. 다각수의 덧셈은?

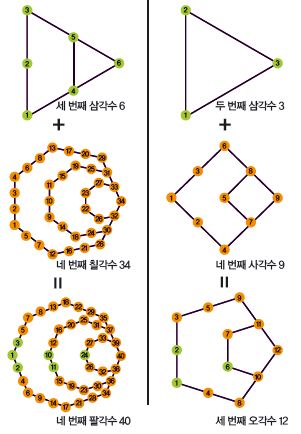
기원전 6세기경 고대 그리스의 수학자 피타고라스가 설립한 피타고라스학파는 수학과 천문을 연구하며, 위대한 업적을 많이 남겼다. 특히 수에 매료돼 다양한 연구를 했는데, 그 중의 하나가 자연수를 도형으로 나타내는 것이다. 즉 점을 이용해 정삼각형, 정사각형, 정오각형, 정육각형으로 나타낸 뒤 삼각수, 사각수, 오각수, 육각수 등으로 부른 것이다. 예를 들어 점 한 개는 첫 번째 삼각수, 점 세 개를 정삼각형으로 배열한 건 두 번째 삼각수, 점 6개를 정삼각형으로 배열한 건 세 번째 삼각수라고 불렀다.
그런데 이런 다각수를 서로 더하면 어떤 모양이 될까?
멕시코의 물리학자 엔리케 젤레니는 삼각수와 사각수, 삼각수와 칠각수 등을 더해 보았고, 오른쪽과 같은 결과를 얻었다.