d라이브러리

고대 그리스 때부터 수학자들은 소수를 모든 수의 근원으로 봤다. 먼 옛날 고대 그리스 철학자인 데모크리토스는 ‘그 이상 분해할 수 없는 것’이라는 의미의 원자(atom)가 다양한 물질을 만드는 궁극의 단위라고 생각했다. 마찬가지로 소수는 다양한 수를 만드는 궁극의 단위로 여겨졌다. 

과거 정수론은 실용적이지 않은 분야로 생각돼 왔다. 그런데 수를 기반으로 하는 컴퓨터가 발달하면서 정수론을 이용해 여러 컴퓨터 기술을 만들 수 있다는 실용성이 입증돼 최근에는 활발하게 연구하고 있다. 특히 소수는 암호와 보안에 많은 역할을 함으로써 소수 연구에 많은 학자가 뛰어들고 있다. 암호에 관한 소수 이야기는 Chapter5(76쪽 부터)에서 자세히 다룬다. 

불규칙해서 더 궁금한 소수 

앞서 소수교의 정시우 학생은 소수가 불규칙해서 더 알고 싶고 매력적인 존재로 느껴진다고 말했다. 오늘날까지 많은 수학자도 정확히 이 점 때문에 소수 연구에 매달린다. 소수는 수학자에게 가닿을 듯, 가닿을 수 없는 느낌을 준다. 

간단한 질문이다. 수천 년 전부터 수학자들은 소수를 향해 이런 질문을 던져왔다. 그러나 여전히 풀리지 않고 있다. 일단 첫 번째 질문부터 답을 구하지 못했기 때문에, 다음 질문도 명확히 풀리지 않고 있다. 

소수는 아무런 규칙 없이 무작위로 드문드문 나온다. 그런데 왠지 조금만 더 큰 소수를 찾으면 규칙을 발견할 것 같은 예감이 들게끔 수가 등장한다. 

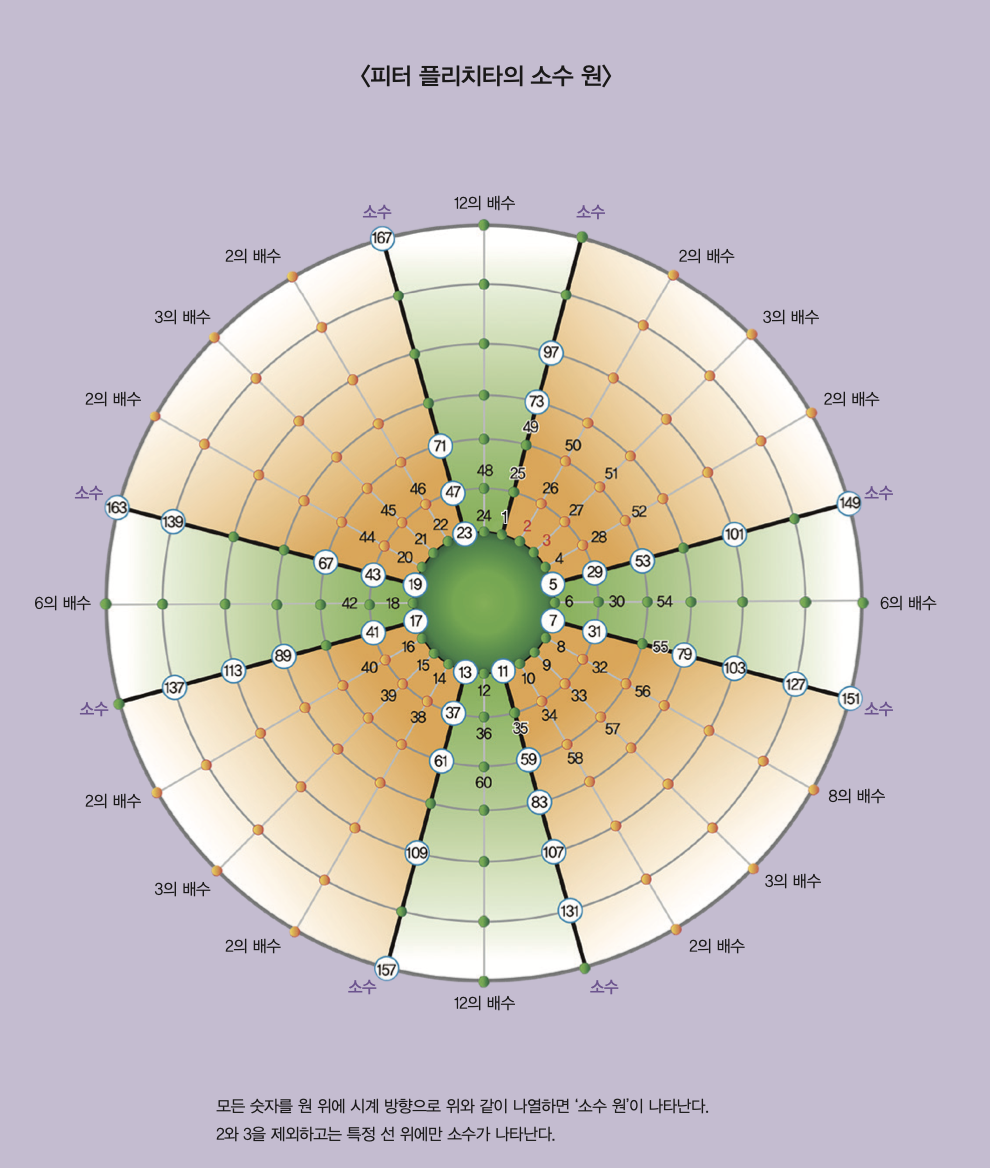
오른쪽 그림은 1998년 독일의 화학자이자 작가인 피터 플리치타가 만든 ‘소수원’이다. 자연수를 1부터 순서대로 동심원 위에 시계 방향으로 나열하면 이 같은 그림이 나타난다. 숫자 24개마다 한 줄 밖의 원으로 이동하도록 설계돼 있고, 소수는 흰색 원 안에 표기했다. 그러자 소수는 2와 3을 제외하고는 특정 선 위에만 나타난다는 사실을 알게 됐다. 하지만 여기까지. 각 직선을 보면 전혀 규칙성이 보이지 않는다. 

규칙성을 찾을 수 있을 듯 말 듯 한다. 이런 실낱같은 희망이 연구를 계속하게 만든다. 지금도 많은 수학자가 이런 소수의 마력에 빠져 연구하고 있다.