d라이브러리

고대 그리스의 수학자 에라토스테네스는 소수를 구하는 방법을 깊이 연구했다. 에라토스테네스는 수학자이자 철학자로 시, 천문학, 지리학, 수학 등 다양한 분야에서 업적을 남긴 인물이다. 

그가 소수를 확실하게 발견하기 위해 고안한 방법은 ‘에라토스테네스의 체’다. 이 방법은 매우 단순하지만, 오늘날까지 확실하게 소수를 발견하는 이 이상의 방법이 없다. 그의 방법을 한 번 살펴보자.

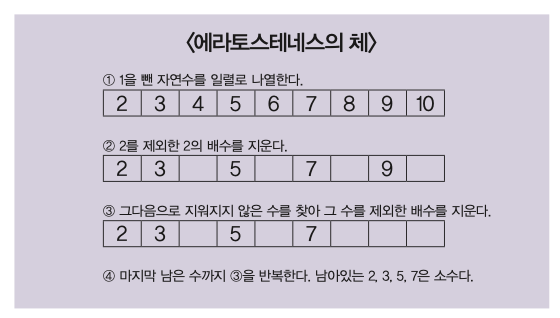
100보다 작은 소수를 모두 찾고 싶다고 하자. 먼저 1부터 100까지 자연수를 모두 적는다. 1은 소수도 합성수도 아니므로 지운다. 2는 1과 자기 자신으로만 나뉘는 소수이므로 동그라미를 치며, 2를 뺀 2의 배수 모두를 삭제한다. 

남아 있는 수 중 아직 동그라미가 그려지지 않은 가장 작은 수를 찾아 동그라미를 치고, 그 수의 2배, 3배, 4배…가 되는 수를 모두 지운다. 이 작업을 계속 반복한다고 생각해보자. 결국 마지막에는 2, 3, 5, 7, 11, …처럼 소수만 남을 것이다. 이게 바로 에라토스테네스가 고안한 소수 판정법 에라토스테네스의 체다.

더 시야를 넓혀 에라토스테네스의 체를 이용해 N 이하의 자연수 중에서 소수를 찾아보자. 커다란 종이에 N까지 자연수를 모두 적는다. 먼저 1을 지운 뒤, 남아 있는 가장 작은 수에 동그라미를 치고 그 수를 뺀 배수는 모두 지우다. 이 과정을 반복한 뒤 가장 작은 수가 √N을 넘으면 이 행위를 멈춘다. 어떤 수가 합성수라면 √N 이하면서 1과 자기 자신이 아닌 약수를 반드시 가지기 때문에 남은 수는 소수가 된다. 정리하면 소수를 찾기 위해 동그라미를 치고 지우는 작업은 많아야 √N 까지만 하면 된다. N까지의 소수를 구하려면 √N 까지의 소수를 체에 거르기만 해도 충분하다는 명제가 증명된 것이다. 

이 방법은 오늘날까지 수학과 컴퓨터 과학에서 중요한 기술로 쓰이고 있다.