d라이브러리

소수를 수학자들이 언제부터 연구했는지는 확실하지 않다. 인류의 소수 사랑은 1950년 아프리카 콩고에서 발견된 동물의 뼛조각에서 살짝 엿볼 수 있다. 기원전 6500년경 구석기 시대 유물인 ‘이상고 뼈’에는 날카로운 줄무늬가 촘촘히 새겨져 있었다. 학자들은 그 줄무늬가 11, 13, 17, 19 네 개의 수를 의미한다고 해석했다. 이는 10과 20 사이의 소수로, 수천 년 전 사람들이 이미 소수의 개념을 알고 있었다고 추측하게 만든다.

또 기원전 1000년 경 중국의 청동기 시대 사람들은 콩을 다섯 개씩 세 줄로 늘어놓아 5라는 소수로 15를 만들 수 있다는 기록을 남겼다. 

남아 있는 기록에 따르면 인류가 본격적으로 소수를 연구 주제로 삼은 시기는 고대 그리스다. 고대 그리스인들은 소수를 이용해 어떤 수든 만들 수 있다는 성질을 신비롭게 여겨 소수를 모든 수의 근원으로 여겼다. 만물이 물과 불, 흙, 공기로 창조됐다고 생각한 그들의 세계관을 수로 확장해 소수를 중심에 둔 것이다.

특히 2000년 전 에우클레이데스는 오늘날 많은 수학자가 ‘가장 아름다운 증명’으로 꼽고 있는 소수 명제를 증명한다. 바로 소수가 무한하다는 사실을 증명한 ‘소수의 무한성 정리’다. 

에우클레이데스는 기원전 3세기 무렵 이집트의 알렉산드리아에서 활약했던 수학자다. 당시 그가 쓴 저서 <;원론>;은 오늘날까지 읽히는 역사상 가장 유명한 수학 교과서다. 에우클레이데스는 이 <;원론>;에서 아주 간단하게 소수가 무한하다는 사실을 증명했다.

에우클레이데스의 소수 무한성 정리

에우클레이데스의 증명을 자세히 살펴보면, 먼저 p를 이 세상에서 가장 큰 소수라고 가정한다. 즉 소수가 2, 3, 5, 7,…, p 라는 식으로 유한한 개수밖에 없다고 생각한다. 그리고 이 유한한 개수의 소수를 모조리 곱한 다음 1을 더한다. 이 값은 소수가 아닌 합성수다. p를 세상에서 가장 큰 소수로 가정했기 때문에 p + 1은 소수일 수 없다. 

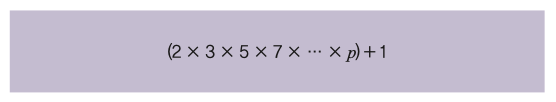
그렇지만 합성수는 소수를 곱해서 만들어지므로 반드시 어떤 소수로 나눠떨어진다. 그 수를 2, 3, 5, 7, …, p라는 식으로 모든 소수의 순서대로 나눈다면 반드시 1이 남는다. 왜냐하면 2 × 3 × 5 × 7 × … × p는 나머지 없이 나눠떨어지지만, 거기에 다시 1을 더했기 때문이다. 다시 말해 이 수는 어떤 소수로도 나눠떨어지지 않는다.

결국 이 수는 합성수가 아닌 소수라는 결론에 도달한다. 문제는 그렇게 되면 p보다 큰 소수를 발견한 셈이므로, ‘p가 가장 큰 소수’라는 최초의 가정과 정확히 모순된다. 치명적인 모순이 발생했으므로, 처음 가정은 더는 성립하지 않는다. 그러므로 소수는 무한하다는 결론이 나온다.

에우클레이데스는 증명하려는 명제의 결론을 부정한 뒤 모순을 이끌어 증명하는 ‘귀류법’으로 소수가 무한하다는 것을 보인 것이다. 소수가 무한하다면 세상에서 가장 큰 소수는 있을 수 없으니 말이다.

이 증명에 대해 이승재 인천대학교 수학과 교수는 “어떤 소수의 집합이 있어도 그 소수들로 나눠지지 않는 수를 아주 간단하고 쉽게 만들었다”라면서, “‘어떤 것이 무한하다’는 추상적인 명제를 기원전 3세기경의 사람이 이런 발상으로 증명했다는 것 자체가 아릅답게 느껴진다”라고 설명했다. 

에우클레이데스로 인해 소수가 무한하다는 것을 21세기를 사는 우리도 의심하지 않을 수 있게 증명해냈다. 증명의 힘이 이래서 강하다.