d라이브러리

양쪽 눈도 거울로 자세히 들여다보면 그 크기나 모양이 다르고, 일란성 쌍둥이도 자세히 보면 키나 생김새가 조금씩 다른 것을 알 수 있다. 이처럼 생활 속에서 쓰는 ‘똑같다’라는 말은 상황에 따라 조금씩 오차가 있기 마련이다. 그렇다면 수학에서 똑같다는 말은 어떻게 표현할까? 수학에서는 도형이나 식이 같은 경우 각각 합동과 등호로 표현한다.

 

 

우선 합동은 모양과 크기가 똑같아서 서로 완전히 포개어지는 도형을 말한다. 기호로 ‘≡’를 사용하는데, 예를 들어 삼각형 ABC와 삼각형 DEF가 합동이면 △ABC ≡ △DEF라고 쓴다. 

 

≡는 어떻게 합동을 나타내는 기호로 쓰이게 된 걸까? 사실 19세기까지만 해도 합동을 나타내기 위한 기호로 ≡보다 ≅를 더 많이 사용했다. ≅는 1824년 독일의 수학자 카를 몰바이데가 처음 사용했다. 그런데 몰바이데 역시 이 기호를 독창적으로 만들었다기보다는 1710년 라이프니츠가 사용한 기호 ≃에서 따왔다고 볼 수 있다.

 

≡를 처음으로 사용한 건 1801년 독일의 수학자 카를 프리드리히 가우스였다. 하지만 가우스는 도형의 합동이 아닌 ‘정수론에서의 합동’ 관계를 나타내기 위해 ≡를 사용했다. ‘두 정수 a, b에서 그 차가 정수 m으로 나눠떨어질 때 a, b와 m을 mod로 하여 합동’이라고 하며, 이를 ‘a ≡ b(mod m)’라고 쓴다. 즉, 기호 ≡는 정수론에서의 합동으로 주로 사용되다가 점차 도형의 합동을 나타내는 데에도 쓰이게 됐다. 

 

한편 모양은 같지만 크기가 다른 도형은 ‘닮음’이라고 한다. 어떤 도형을 일정한 비율로 키우거나 줄이면 처음 도형과 ‘닮음’인 도형을 만들 수 있다. 닮음 기호로는 ∽를 사용하는데, ∽의 원조 역시 라이프니츠로 추정된다. 라이프니츠는 1679년 한 원고에서 닮음을 나타내기 위해 ∽와 비슷한 모양의  또는 이와 상하가 반대인 ∼를 사용했다고 전해진다. 라이프니츠는 ‘닮음’이란 뜻의 라틴어 similis의 첫 자인 S를 변형해 닮음 기호를 만든 것으로 알려졌는데, 그의 원고가 현재 남아 있지 않아 정확히  ∼ 를 썼는지, ∼를 썼는지는 확실치 않다. 

 

 

 

둘 이상의 수나 식이 서로 같다는 것을 나타낼 때는 등호 ‘＝’를 사용한다. 등호의 원조는 영국의 수학자이자 의사인 로버트 레코드다. 그는 영국 옥스퍼드대학교에서 수학을 가르치면서도 궁정에 초빙돼 에드워드 6세와 메리 여왕의 주치의를 지낼 정도로 유능한 의사였다. 또 천문학에도 조예가 깊어 영국 최초로 코페르니쿠스의 지동설을 이해하고 이를 주장한 사람으로도 잘 알려졌다. 

 

그는 여러 권의 수학책을 집필했는데, 1557년에 쓴 영국 최초의 대수학책 <지혜의 숫돌>에서 세계 최초로 등호 =를 사용했다.

 

 

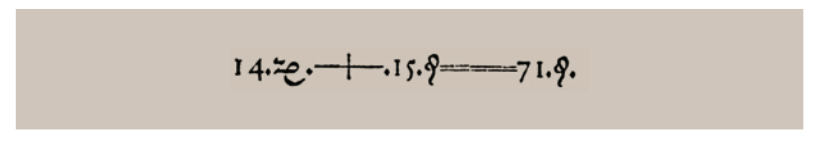
레코드의 등호는 위의 수식처럼 현재의 등호보다 매우 긴 형태인데, 그는 자신의 책에 =를 소개하며 다음과 같은 글을 썼다. 

 

‘‘같다’라는 단어가 지루하게 반복되는 것을 피하고자, 길이가 같으면서도 평행해 마치 쌍둥이 같은 두 직선  ==============을 사용할 것이다.’

 

이 글은 수학에서 기호가 만들어진 이유와 그 중요성을 나타내고 있다. 기호를 사용함으로써 긴 문제도 간략하게 표현할 수 있게 된 것이다. 또 기호는 언어에서 발생하는 오해의 소지도 없앨 수 있다. 

 

우리가 생활 속에서 흔히 쓰는 ‘똑같다’라는 말은 사실 완전히 똑같지 않을 때도 쓰지만, 수학에서 ≡, ＝가 쓰였다면 절대적으로 같은 것을 의미하기 때문이다.

 

 

레코드의 고향 영국 웨일스 펨브로크셔주 텐비에 세워진 성 메리 교회에는 그의 업적을 기리는 기념비가 세워져 있다.