
수학 문제를 풀다 보면 숫자 외에도 각종 기호를 만난다. 수학에선 개념을 기호로 추상화해 쓰기 때문이다. 수학이 ‘기호의 학문’이라고 불리는 이유다. 그런데 기호마다 사용에 이르기까지 유구한 역사가 있다. 기호의 역사를 살펴보며 기호 속에 담긴 개념에 대해서도 깊이 알아보자.
당신이 태어나서 가장 처음 푼 수학 문제에 등장한 기호는 무엇이었을까. 아마 +와 이지 않을까. 이 두 기호는 수학 문제에서 가장 기본이 되는 기호다. 그래서 숫자의 탄생과 함께 고대부터 있었을 것 같지만, 지금과 같은 형태를 갖춘 역사는 생각보다 매우 짧다. 대체 누가, 언제부터, 어떻게 +와 -를 쓰기 시작한 걸까.
수를 사용하기 시작한 것은 기원전 6500년경이라고 전해진다. 당시 유물인 ‘이상고 뼈’에 인류가 셈을 기록한 흔적이 있다. 초기에는 세고자 하는 물건을 작대기와 일대일 대응하는 것으로 시작해 점차 체계적인 수 체계를 형성했다. 고대 이집트나 바빌로니아, 마야, 인도 등의 수체계가 대표적이다.
수체계가 발전을 거듭하는 사이, 기호는 천천히 탄생했다. 이때만 해도 기호가 없으니 문장으로 쓰는 수밖에 없었다. 7 + 8을 ‘칠 더하기 팔’이라고 쓰는 것처럼, 요즘 말로 문장제 문제를 읽고 푼 것이다.
사람들은 자주 쓰는 수량이나 계산을 빨리 적기 위해 단어를 점차 짧게 줄여 사용하기 시작했다. 그러다가 축약된 글자마저 사라지고 드디어 기호만 남게 됐다. 대부분의 수학 기호는 이렇게 문장 형태에서 축약 단계 그리고 기호의 단계를 거쳐 탄생했다.
인류 최초로 수학 기호 사용한 디오판토스
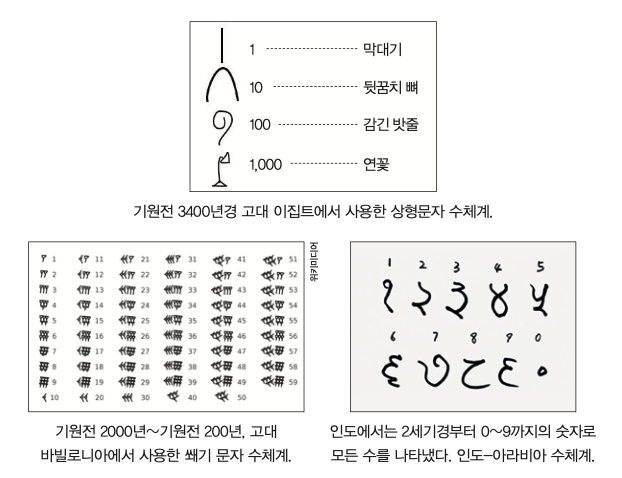
현재까지 밝혀진 역사에 따르면 인류 최초로 수학 기호를 사용한 사람은 3세기 고대 그리스의 수학자 디오판토스다. 그는 문장으로 쓰던 방정식을 미지수와 나누기, 빼기 기호를 사용해 단순한 수식으로 표현했다. 11세기경 인도에서는 더하기를 산스크리트어 음가 중 하나인 ‘야(या)’로 쓰고, 빼기는 숫자 위에 점을 찍어 표기한 기록이 남아 있다.
디오판토스가 사용한 기호
하지만 기호란 쓰이지 않으면 아무 소용이 없는 법. 디오판토스의 기호와 인도의 더하기, 빼기 기호는 받아들여지지 못하고 기호 탄생의 순간은 몇 세기 뒤로 밀려나고 만다.
유럽에서는 476년 서로마제국이 멸망하고, 1453년 비잔티움(동로마) 제국이 멸망한 이후에도 로마의 공용어인 라틴어가 뿌리 깊게 자리잡고 있었다. 그래서 빼기의 경우 ‘모자라다’라는 뜻의 라틴어 미누스(minus)가 그대로 사용됐다. 그러다가 단어를 줄여 글자 m 위에 줄을 그은 표시가 15세기까지 사용됐다. 이후 글자도 사라지고 위에 그은 줄만 남은 것이 바로 - 기호다.
+ 기호도 비슷한 변화 과정을 거쳐 탄생했다. +는 ‘그리고’라는 뜻의 라틴어 에트(et)를 흘려 쓰는 과정에서 점점 축약돼 만들어졌다.
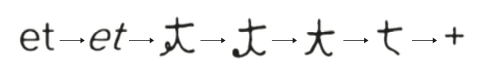
+와 -가 공식적으로 등장한 것은 1489년 독일의 수학자 요하네스 비트만의 책에서다. 비트만은 +와 -를 지금처럼 연산 기호로 사용한 것이 아니라, 물건 계산을 할 때 ‘너무 많다’와 ‘모자라다’라는 뜻을 전달하기 위해 사용했다. 이것을 연산 기호로 처음 사용한 사람은 1514년 네덜란드의 수학자 판 데르 후커였다. 이후 여러 수학자의 노력에 의해 +, - 표기법이 자리잡게 된다.
+와 - 탄생 이후, 16세기 유럽에서 여러 수학 기호들이 하나둘 모습을 드러내기 시작한다. 기호가 등장하며 수학은 문장 형태에서 명료한 기호의 체계로 탈바꿈한다. 기호가 수학의 새로운 시대를 연 것이다.

1489년 출판된 독일의 수학자 요하네스 비트만의 책으로, 이는 +와 가 공식적으로 처음 인쇄된 책이다.
x를 닮은 , 그 기원은?
인류는 상당히 오랜 옛날부터 곱셈 계산을 한 것으로 알려졌지만, 곱셈 개념을 처음으로 만든 사람이 누구인지는 정확히 모른다. 다만, 기원전 2000년경 고대 이집트와 바빌로니아 시대 유적에 곱셈에 대한 최초의 기록이 남아 있다. 고대 이집트인들은 2배 하기와 10배 하기를 통해 곱셈을 계산했고, 고대 바빌로니아인들은 곱셈표를 이용했다.
현재 우리가 사용하고 있는 곱하기 기호 는 생각보다 늦게 등장했다. 앞서 +와 -가 공식적으로 등장한 시기를 1489년이라고 소개했는데, 가 등장한 건 이보다 약 140년이나 지난 1631년이다.

1631년 영국의 수학자 윌리엄 오트레드는 저서 <수학의 열쇠>에서 곱하기 기호 ‘’를 처음 사용했다. 그는 1622년 계산자를 발명한 것으로도 잘 알려졌다. 계산자란 곱셈이나 나눗셈뿐만 아니라 암산하기 어려운 복잡한 수의 계산도 가능케 하는 도구로, 전자계산기나 컴퓨터가 등장하기 전까지 과학자와 기술자들에게 계산 필수품이었다.
하지만 안타깝게도 오트레드가기호를 어떻게 만들었는지는 정확히 알려지지 않았다. 는 그 모양이 미지수를 나타내는 문자 x와 닮아 헷갈린다는 이유로 많이 쓰이지 않다가 19세기 후반이 돼서야 널리 사용되기 시작했다.
오트레드 이전에도 사용한 기호
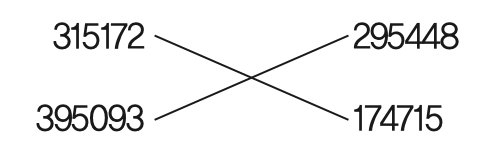
4개의 숫자 사이로 거대한 기호가 눈에 띈다. 이 계산은 1551년 오스트리아의 인문학자이자 천문학자인 에라스무스 오스왈드 슈레켄푸흐스가 사용했다. 그는 고대 그리스의 수학자이자 천문학자인 클라우디오스 프톨레마이오스의 저서 <천문학 집대성>을 번역하며 위와 같은 곱셈식을 썼다. 슈레켄푸흐스의 는 현재 사용하는 것과 같은 곱하기 기호가 아니다. 315172와 174715를 곱하고, 295448과 395093을 곱하라는 의미로 쓰였다.
편리한 곱셈 기호, •의 탄생
곱하기 기호로외에 •도 있다. 예를 들어 6과 4의 곱이나와 -9의 곱은 각각 6•4 = 24, (-5)•(-9) = 45와 같이 나타낼 수 있다.
•기호를 처음 사용한 건, 영국 과학자이자 수학자인 아이작 뉴턴과 함께 미적분을 발명한 독일 수학자 고트프리트 라이프니츠다. 라이프니츠는 1676년 한 원고에서 곱하기 가 미지수 x와 닮아 헷갈린다는 이유로 널리 쓰이지 못했다고 적었다. 실제로 라이프니츠는 1698년 7월, 스위스 수학자 요한 베르누이에게 다음과 같은 편지를 보냈다.
‘기호 는 문자 x와 혼동되기 때문에 곱하기를 나타내기 위한 기호로 를 사용하지 말고 대신 •(점)을 쓰자.’
영국의 수학자이자 천문학자인 토마스 해리엇은 1631년 출간한 저서 <해석학의 실제>에서 •을 썼다. 하지만 •을 곱하기로 사용했다기보다 수와 문자를 구별하기 위해 을 사용했던 옛 필사본의 관습을 따른 것으로 보인다. 오늘날에는 곱하기 기호로 ×와 •을 모두 사용한다. 이 기호는 수백 년에 걸쳐 곱셈을 간결하게 표현하기 위해 고민한 수학자들의 약속이다.
상형문자의 원리로 만든, ÷
‘해’를 뜻하는 한자 日(날일)은 해의 모양을 본떠 만들어졌다. 또한  는 사람의 형상을 본떠 만든 고대 이집트 문자다. 이처럼 그 사물의 형상을 본떠 단어나 소리를 표현하는 문자를 ‘상형문자’라고 하는데, 초기 한자와 고대 이집트 문자에서 나타나는 특성이다. 그런데 상형문자와 비슷한 원리로 탄생한 수학 기호가 있다. 바로 나누기 기호다.
는 사람의 형상을 본떠 만든 고대 이집트 문자다. 이처럼 그 사물의 형상을 본떠 단어나 소리를 표현하는 문자를 ‘상형문자’라고 하는데, 초기 한자와 고대 이집트 문자에서 나타나는 특성이다. 그런데 상형문자와 비슷한 원리로 탄생한 수학 기호가 있다. 바로 나누기 기호다.
초등학교 때는 숫자를 나눌 때 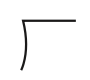 기호를 사용한다. 예를 들어 24 나누기 8은 아래쪽과 같다. 나누는 과정이 분명히 드러나 처음 나누기를 배울 때 편리하게 셈을 익힐 수 있다. 이런 나누기 기호
기호를 사용한다. 예를 들어 24 나누기 8은 아래쪽과 같다. 나누는 과정이 분명히 드러나 처음 나누기를 배울 때 편리하게 셈을 익힐 수 있다. 이런 나누기 기호 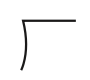 는 언제 처음 사용했을까?
는 언제 처음 사용했을까?
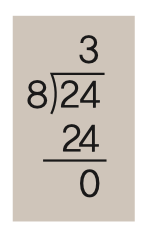
이 기호의 원조는 1544년 출간된 독일의 수학자 미하엘 슈티펠의 저서 <산술백과>에서 처음 등장한다. 24 나누기 8을 ‘8)24’ 또는 ‘8)24(’로 나타냈다.
그렇다면 나누는 수 위의 선은 어떻게 생긴 걸까? 그 기원은 분명히 알려져 있지 않지만, 훗날 나누는 수를 분명하게 표시하기 위해 슈티펠의 기호 ‘)’ 위에 선 ‘ ̄’을 덧붙여 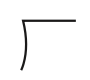 기호가 만들어진 것으로 추정된다. 슈티펠의 기호를 그냥 사용할 경우 ‘2)4x - 7’이라는 식이 ‘‘(4x - 7) ÷ 2 ’를 말하는 건지, ‘(4x ÷ 2) -7’을 말하는 건지 정확히 알 수 없기 때문이다.
기호가 만들어진 것으로 추정된다. 슈티펠의 기호를 그냥 사용할 경우 ‘2)4x - 7’이라는 식이 ‘‘(4x - 7) ÷ 2 ’를 말하는 건지, ‘(4x ÷ 2) -7’을 말하는 건지 정확히 알 수 없기 때문이다.
한편 라이프니츠는 1684년 독일의 첫 번째 과학 저널 <학술기요>에서 비율과 나누기를 나타낼 때 :(콜론)을 사용했다. 하지만 이 기호는 나누기 기호로서 널리 받아들여지지 못했고 결국 사용되지 않고 있다.
재미있는 것은 현재 가장 많이 쓰이고 있는 기호 ÷가 나누기 기호로 정착되기 전, 이미 많은 수학자에 의해 다른 뜻으로 사용됐다는 점이다. 유럽의 수학자들은 ÷를 빼기를 나타내는 기호로 오랫동안 사용했다. 심지어 스칸디나비아의 몇몇 국가에서는 이 기호를 20세기까지 빼기로 썼다. 하지만 영어를 사용하는 국가에서는 이 기호를 항상 나누기로만 사용했다.
밝혀진 바에 따르면 ÷는 1659년 스위스의 수학자 요한 란의 저서 <대수학>에서 처음 나누기 기호로 쓰였다. 그는 나누기 기호뿐만 아니라 ‘그러므로’를 뜻하는 수학 기호 ∴도 처음 사용한 것으로 잘 알려졌다.
그렇다면 ÷는 어떻게 나누기를 나타내는 데 쓰였을까? 한 가지 주장에 따르면기호에서 가로 막대 ─ 위아래의 두 점이 수를 나타낸다고 한다.
예를 들어 35 ÷ 23은 35/23와 같은 분수 형태로 나타낼 수 있는데, 기호 ÷가 이 분수의 모양을 추상화한 거라는 뜻이다. 가로 막대 ─ 위에 있는 35와 아래에 있는 23을 각각 ·으로 바꾸면 나누기 기호 ÷가 된다.












