수학에서 가장 중요한 상수를 뽑으라고 하면? 많은 사람이 원주율 π를 쉽게 떠올릴 것이다. 실제로 수학자들은 π가 3.141592임을 기념하기 위해 3월 14일을 파이 데이로 정하고, 이를 축하하는 여러 행사를 연다. 그렇다면 이 유명한 기호 π는 대체 어떻게 탄생한 것일까?
원주율은 원의 지름에 대한 둘레의 비율을 나타내는 상수다. 그런데 원주율의 값은 3.1415926535897…로 딱 떨어지지 않고 소수점 아래 수가 무한히 계속된다. 이처럼 순환하지 않는 무한소수를 ‘무리수’라고 한다.
무한히 계속되며 순환하지 않는 소수인 원주율을 정확히 구하기 위한 수학자들의 노력은 고대부터 오늘날까지 계속되고 있다. 맨 처음 등장한 π의 근삿값은 3이었다. 약 5000년 전 고대 메소포타미아(고대 페르시아)에서 원주율이 3으로 쓰였고, 고대 중국의 수학책인 <구장산술>에도 원주율을 3으로 계산한 기록이 남아 있다.
하지만 또 다른 문명의 발상지인 이집트는 달랐다. 기원전 1850년경 고대 이집트인이 남긴 린드 파피루스 기록에는 이집트인들이 구한 원의 넓이 공식이 나온다. 그 기록을 오늘날의 방식으로 표현하면 원의 넓이 S는 (16r/9)2이다. 이때 r은 반지름을 의미한다. 이 식과 현재 원의 넓이 공식(= πr2)을 같다고 놓고 원주율을 구하면 이집트인들이 사용한 원주율은 ‘3.1604…’가 된다. 다른 문명과 비교하면 놀라울 정도로 정밀한 결과다.

약 1600년의 세월이 흐르고 나서야 이를 뛰어넘는 계산을 한 수학자가 등장한다. 그 주인공은 아르키메데스였다. 그는 원에 외접하는 정다각형과 내접하는 정다각형을 이용하는 방법을 고안했다. 원의 둘레는 외접하는 정다각형의 둘레보다 길이가 짧고, 내접하는 정다각형의 둘레보다는 길다고 생각한 거다.
아르키메데스는 원에 외접하고 내접하는 정96각형 두 개를 이용해 원주율이 223/71과 22/7 사이에 있음을 알아냈다. 사실 이 시기에는 소수의 개념이 없어 분수로 값을 표기했다. 이를 소수점 셋째 자리에서 반올림할 경우 약 3.14가 된다. 우리가 학교에서 계산할 때 사용하는 소수점 아래 2번째 자릿수까지의 원주율을 아르키메데스가 완성한 것이다.
아르키메데스가 원주율을 구한 계산법은 사람들에게 널리 알려졌고, 그 결과 오늘날까지 원주율을 ‘아르키메데스 상수’라고 부르기도 한다.
아르키메데스의 다각형법
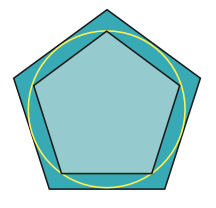
기원전 250년경, 아르키메데스는 정다각형의 변의 개수를 늘려가며 원에 내접하고, 외접하는 정다각형을 그려나갔다. 결국 정96각형을 이용해 원주율이 약 3.14임을 확인했다.

3.141592까지 알아낸 조충지
인류 최초로 원주율의 소수점 아래 6번째 자릿수까지 정확하게 알아낸 사람은 중국의 수학자였다. 바로 기원후 429년부터 500년까지 중국 남북조시대 송나라에 살았던 수학자 조충지다. 그는 천문학 계산이나 토지 측량의 정확도를 높이기 위해 원주율 계산에 매달렸다. 480년경 정24576각형을 이용해 원주율이 3.1415920과 3.1415927 사이에 존재하는 것을 알아냈다.
3.141592는 1969년 인류가 처음 달에 가기 위한 아폴로 계획을 수행할 때 계산에 적용한 원주율 근삿값이며, 원주율을 소수점 6자리까지 구한 이 값은 현대 공학 계산에서 널리 활용된다.

중국에서 전해진 수학을 바탕으로 중세 이전 가장 정확한 원주율을 찾은 사람은 15세기 아라비아(현재 중동) 지역의 수학자 잠시드 알-카시다. 그는 정85306368각형을 이용해 원주율의 소수점 아래 14번째 자릿수까지 정확하게 구했다. 16세기 후반에 이르기까지 어떤 수학자도 알-카시가 구한 것보다 더 정확한 값을 제시하지 못했다.
그 후 1596년 네덜란드 수학자 뤼돌프 판 쾰런은 저서 <원에 대하여>에 원주율을 소수점 아래 20번째 자릿수까지 계산한 결과를 실었다. 25년 뒤인 1621년에는 약 461경 개 이상의 변으로 이뤄진 정다각형을 이용해 소수점 아래 35번째 자릿수까지 계산하는 데 성공했다.
급수로 원주율 구하는 시대 연 인도 수학자
아르키메데스가 제안한 방식처럼 도형을 이용하는 원주율 계산법은 15세기 인도의 수학자 산가마그라마 마다바가 무한급수 중 ‘아크탄젠트(arctanx) 급수(수열의 합)’를 발견하면서 끝난다. 이후부터 본격적으로 급수로 원주율을 구하는 시대가 열린 것이다. 아크탄젠트 급수란 탄젠트의 역함수를 무한급수로 표현하는 수식이다.
흔히 숫자로 이뤄진 항을 나열한 것을 수열이라고 한다. 이 수열의 모든 항을 덧셈이나 뺄셈으로 연결한 것을 ‘급수’라고 하며, 항의 개수가 유한하면 유한급수, 무한하면 무한급수라고 부른다.
1671년 스코틀랜드의 수학자 제임스 그레고리는 마다바의 발견 사실을 모른 채 같은 결과인 아크탄젠트 급수를 알아냈다. 또 1676년 라이프니츠는 아크탄젠트 급수의 변수 x에 1을 대입해 최종적으로 아래와 같은 원주율 계산식을 고안했다.
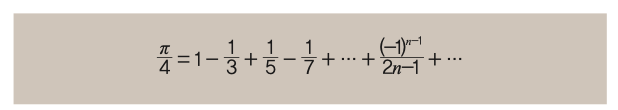
이 식의 우변은 1과 1/3, 1/5 처럼 분모가 홀수고 분자가 1인 분수를 순서대로 더하고 빼는 과정을 무한히 반복한다는 의미다. 하지만 이 방식으로는 300번째 항까지 계산해도 원주율이 소수점 아래 2번째 자릿수까지만 정확하게 나온다는 한계가 있었다.
아크탄젠트 급수는 ‘그레고리 급수’나 ‘라이프니츠 급수’ 등의 이름으로도 불린다. 상대적으로 마다바보다 두 사람의 이름을 딴 급수가 더 많이 알려졌다.
17세기 후반 뉴턴은 아크사인(사인의 역함수) 급수의 변수 x에 1을 대입해 얻은 ‘뉴턴 급수’를 고안한다. 뉴턴 급수는 22번째 항까지만 계산해도 원주율의 소수점 아래 16번째 자릿수까지 정확하게 나온다. 단숨에 라이프니츠 급수의 정확도를 넘어선 것이다.
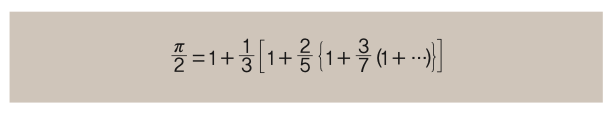
원주율에 도전하는 사람들
원주율을 손으로 계산해서 소수점 아래 수를 가장 많이 알아낸 사람은 영국의 아마추어 수학자 윌리엄 샹크스다. 그는 1873년에 무려 소수점 아래 707번째 자릿수까지 15년에 걸쳐 계산했다고 발표했는데, 이후 컴퓨터 계산을 통해 확인한 결과 527번째 자릿수까지만 정확한 것으로 판명됐다.
현대에 이르러서는 컴퓨터를 이용해 원주율을 계산한다. 원주율을 구하는 알고리듬을 이용하면 일반 컴퓨터로 계산해도 샹크스의 기록을 깨는 데 불과 10분 안팎밖에 소요되지 않는다.
현재까지 원주율 계산 알고리듬 중 가장 빠른 것은 1915년 인도의 수학자 스리니바사 라마누잔이 발표한 초기하급수로 완성한 알고리듬이다.
1946년 미국에서 최초의 진공관 컴퓨터 ‘에니악(ENIAC)’이 개발됐고, 1949년 9월 에니악이 초기하급수로 만든 알고리듬을 활용해 약 70시간 동안 원주율의 소수점 아래 2037번째 자릿수까지 계산하는 데 성공했다. 2005년 야스마사 가네다 일본 도쿄대학교 교수팀은 약 602시간 동안 소수점 아래 1조 2411억 번째 자릿수까지 찾아냈다.
가장 최근 최고 기록은 구글 클라우드 개발자인 이와오 엠마 하루카가 2022년 100조 자리까지 계산한 결과다. 하루카는 2019년 원주율 계산 세계 기록을 세웠지만, 바로 다음 해에 다른 팀에게 빼앗겼다가 2022년에 다시 찾았다.
물론 이 정도로 정확한 원주율은 정밀한 과학 연구나 산업 현장에서도 사용하지 않는다. 되레 다른 계산을 복잡하게 만들 수 있기 때문이다. 우주 연구나 항공 분야에서도 소수점 아래 수십 번째 자릿수의 원주율 근삿값을 사용하고 있다. 결과적으로 원주율 계산은 실사용보다 컴퓨터의 성능을 파악하는 데 쓰이고 있다.
하루카도 2023년 본지와의 인터뷰에서 “개발하고 있는 시스템으로 원주율 계산을 얼마 동안 몇 자리까지 했다고 설명하면, 컴퓨터의 속도나 처리할 수 있는 데이터 크기 등을 개발자가 아닌 사람에게 쉽게 전달할 수 있다”라면서 원주율 계산 세계 기록에 도전하고 있는 이유를 설명했다.

세상에서 가장 아름다운 공식에서 발견되는 π
원주율은 그리스 문자 π로 표기하고 ‘파이’라고 읽는다. 원주율을 나타내는 기호로 π를 처음 사용한 사람은 누구일까? 각도 기호 등 여러 기호를 만든 오트레드는 1647년 원주율을 δ/π로 나타냈다. π를 사용하기는 했지만, 원주율 대신 원의 둘레란 의미로 사용했고, δ는 지름을 나타냈다.
우리가 현재 사용하고 있는 의미로 π를 처음 사용한 사람은 영국의 수학자 윌리엄 존스다. 그는 1706년 출간된 저서 <수학의 새로운 입문서>를 통해 ‘특정 도형의 길이나 넓이를 구하는 계산에 매우 유용한 여러 방법이 있다. 원을 예로 들면 지름이 1인 원의 둘레를 약 3.14159… = π로 표기하는 것이다’라며, 기호 π의 사용을 제안했다. 존스는 둘레를 뜻하는 고대 그리스어 ‘περιφηρής’나 둘레의 길이를 뜻하는 ‘περίμετρον’의 첫 글자를 따서 π를 사용한 것으로 보인다.
하지만 π가 금방 널리 쓰인 것은 아니다. 1740년대까지도 원주율의 기호로 π 대신 다른 문자를 사용하기도 했다. 라틴어 peripheriam(주변)의 첫 글자인 p나 라틴어 circumferentia(원주)의 첫 글자인 c가 그 예다. π가 널리 사용되기 시작한 것은 오일러 덕분이다.
오일러는 당시 유럽에서 매우 영향력 있는 수학자였다. 오일러가 1736년 저서 <메카니카(Mechanica)>서 원주율을 나타내는 기호로 π를 사용하면서부터 원주율을 π로 표기하는 방법이 빠르게 퍼져나가기 시작했다.
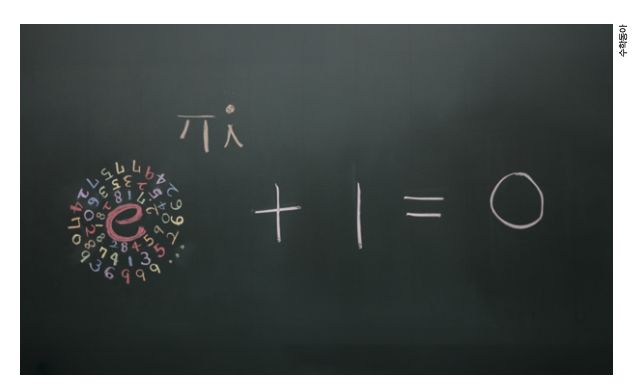
π는 수학자들이 뽑은 가장 아름다운 공식인 ‘오일러 공식(eπi + 1 = 0)’에서도 발견된다. 수학뿐만 아니라 물리학에서 나오는 불확정성의 원리나 동역학 등에서도 π는 그 모습을 드러낸다. 만약 π가 없었다면 어땠을까? 매번 무리수인 원주율을 쓰는 건 여간 곤혹스러운 일이 아니었을 것이다. 또한 가장 아름다운 공식도 만나지 못했을지도 모를 일이다.











