d라이브러리

수학동아 9번째 생일 파티에 오신 여러분 환영합니다. 초대장에 적힌 퀴즈의 정답(99)을 푼 대단한 분들이시군요. 전 김우현 기자가 아니고 마술사 ‘미스터 9’입니다. 제 마술을 도와줄 사람이 필요한데요. 원하는 분은 손을 들어주세요. 아! 거기 모자 쓴 독자 분은 무대 위로 올라와 주세요. 

처음 선보일 마술은 마음을 엿보는 ‘독심술’입니다. 여러분 모두의 마음을 읽어보도록 하죠. 이제부터 제가 말하는 대로 해보세요. 각자 속으로 연속한 세 자연수를 떠올리고, 세 수를 모두 더하세요. 그리고 제곱합니다. 이제 각 자릿수에 있는 수의 합이 한 자리가 될 때까지 계속 더합니다. 제곱해서 256이 나왔으면 2+5+6=13, 1+3=4가 될 때까지 더하라는 뜻이에요. 무대 위에 올라온 독자 분은 떠올린 숫자와 계산 과정을 다른 사람이 볼 수 있게 종이에 적어 주세요. 물론 제가 볼 수 없게요.

자, 계산을 끝낸 것 같으니 이제 독자 분의 마음을 읽어보겠습니다. 여기 1부터 9까지 적힌 숫자 카드에서 독자 분이 계산해 나온 수를 찾아보도록 하겠습니다. 수리수리 마하수리~. 바로 이겁니다, 숫자 9! 독자 분, 종이에 적은 내용을 큰 소리로 읽어주세요.

“저는 5, 6, 7을 떠올렸어요. 세 수를 더하면 18(=5+6+7)이고, 제곱하면 324(=182)가 나와요. 각 자릿수 3, 2, 4를 더하니까 9! 어떻게 아셨죠?”

무대 아래 있는 독자들도 9가 나왔을 거예요. 표정을 보니 무척 놀란 모양이군요. 아직 놀라긴 이릅니다. 더 신기한 ‘예언 마술’이 남았으니까요!

어떤 수를 골라도 결과는 9!

이번에는 수학동아 편집장이 저를 도울 겁니다. 책상 위에 1부터 9까지 적힌 카드가 여러 쌍 있습니다. 똑같은 1쌍이 제 손에도 있지요. 예언 능력을 발휘해 카드를 한 장 고르겠습니다. 이 카드는 5분 뒤에 조가현 편집장이 답할 숫자입니다.

저는 뒤돌아 서 있을 테니 조가현 편집장은 의미 있는 기념일의 년도와 월,일을 각각 두 자리로 나타낸 뒤 숫자 카드에서 골라 차례대로 나열해 주세요. 2018년 10월 1일을 떠올렸다면 ‘181001’이 되겠죠? 이제 카드의 순서를 아무렇게나 섞어 주세요. 그리고 원래 수와 지금 나온 수 중 큰 수에서 작은 수를 빼고, 아까처럼 각 자릿수에 있는 수의 합이 한 자리가 될 때까지 더하세요.

이제 답을 맞힐 시간입니다. 조가현 편집장, 처음에 어떤 기념일을 떠올렸나요?

“중학교 때 좋아했던 아이돌 그룹 ‘신화’의 데뷔일을 생각했어요. 1998년 3월 24일. 즉, 980324죠. 고른 카드를 막 섞어서 324098을 만들었어요. 980324-324098은 656226, 각 자릿수를 더하면 27(=6+5+6+2+2+6), 한 번 더 더해 9(=2+7)가 나왔습니다.”

훗! 보세요. 제가 고른 카드도 9입니다. 짜고 치는 게 아닙니다. 여러분의 생년월일, 혹은 아무 숫자나 골라 해보세요. 답은 언제나 9일 테니까요! 

수학동아 독자 아니랄까봐 몇몇 독자들은 벌써 머리를 맞대고 비밀을 파헤치기 시작했어요. 마술의 비밀을 알려 달라고요? 영업 비밀이라 곤란한데….

마술1 연속한 세 자연수와 3의 배수

궁금하면 잠 못 이루는 독자를 위해 특별히 비밀을 공개 할게요. 항상 답이 9가 되는 숫자 마술은 ‘9의 배수 판정법’을 응용한 거예요. 사실 이 마술은 아이디가 0309인 독자 분이 아이디어를 주셨어요!

첫 번째 마술부터 살펴볼게요. 처음에 ‘연속한 세 자연수’를 고르라고 한 이유가 있습니다. 세 수 중 두 번째로 큰 수가 n이면 가장 작은 수는 n-1, 가장 큰 수는 n+1일 거예요. 이 세 수를 더한 수 3n(=n-1+n+n+1)은 3이 곱해져 있으니까 반드시 3의 배수고, 제곱해서 나온 9n2(=3n×3n)은 9의 배수지요. 

신기하게 9의 배수는 각 자릿수에 있는 수를 더해도 9의 배수가 돼요. 반대로 자릿수에 있는 수의 합이 9의 배수면 9로 나눠보지 않아도 9의 배수인 걸 알 수 있지요. 이걸 ‘9의 배수 판정법’이라고 해요. 

이유가 뭘까요? 10의 거듭제곱은 9로만 이뤄진 수와 1의 합으로 나타낼 수 있기 때문이에요. 예를 들어 1023은 1×103+2×101+3×100으로 쓸 수 있어요. 이는 1×(999+1)+2×(9+1)+3×1이 되고, 정리하면 (1×999+2×9)+(1+2+3)이 되지요. (1×999+2×9)=9×(1×111+2)여서 항상 9의 배수니까 각 자릿수를 더한 1+2+3만 9의 배수면 원래 수도 9의 배수가 되는 거지요!

즉 어떤 세 자연수를 골라도 답은 9뿐이에요!

마술2 예언의 핵심은 10의 거듭제곱!

두 번째 마술에서는 여섯 자릿수로 9를 만들었는데요. 자릿수에 관계없이 어떤 수도 9가 되니 쉽게 세 자릿수로 살펴보겠습니다. 세 자릿수 ABC는 A×102+B×101+C×100으로 쓸 수 있어요. 각 자릿수를 섞어 BCA가 됐다면 이 수는 B×102+C×101+A×100이 되겠죠? A가 B보다 크면 ABC＞BCA이로 큰 수에서 작은 수를 빼면 ABC-BCA=(A-B)×102+(B-C)×10+(C-A)×100이에요. 이 값을 정리하면 A(102-100)+B(101-102)+C(100-101)이 됩니다. 

지수는 다르지만, A, B, C에 모두 10a-10b 꼴의 수가 곱해진 게 보이나요? 마술1에서 본 것처럼 10의 거듭제곱은 10=9+1, 100=99+1, 1000=999+1 같이 10n=9…9+1로 쓸 수 있어요.

그런데 9…9는 9×1…1이라 항상 9의 배수예요. 즉10a-10b은 (9…9+1)-(9…9+1)=9×(1…1-1…1)이므로 9의 배수고 여기에 A, B, C를 곱해도 9의 배수지요. 그래서 이 마술의 결과는 언제나 9가 나오는 거예요.

● 조혜인 기자를 구하라! 

안녕하세요! 미스터 9의 조수 ‘미스 뷔’입니다. 오늘만큼은 저도 박현선 기자가 아닌 마술사랍니다. 가장 신기한 마술 중 하나가 절단 마술이죠? 여기 상자 안에 들어가 있는 조혜인 기자의 몸을 둘로 나눠보겠습니다. 하나, 둘, 셋!

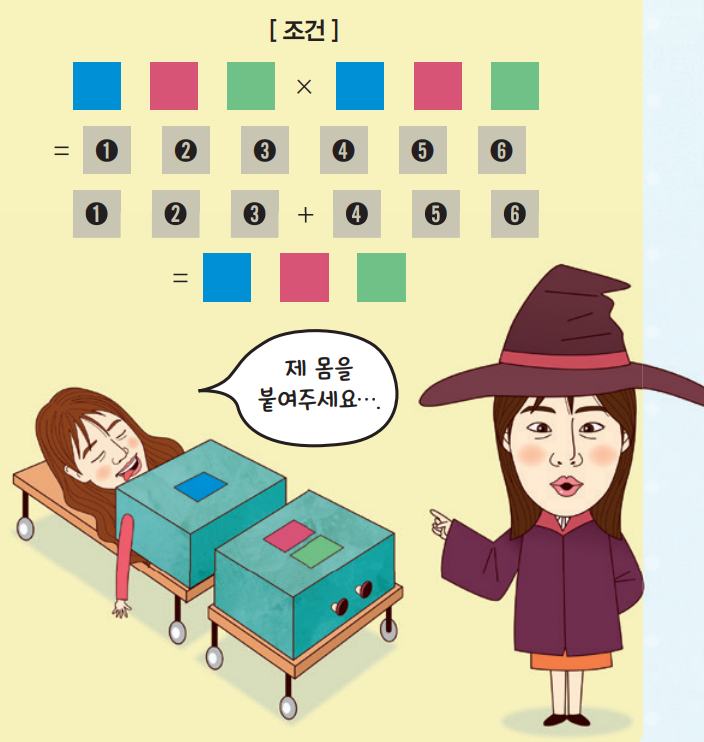
어이쿠, 어쩌죠? 제가 실수를 하고 말았어요. 상자에 든 조혜인 기자는 무사할까요? 독자 여러분의 힘을 합치면 조혜인 기자를 구해낼 수 있답니다. 여기 상자에 붙은 파란색, 빨간색, 초록색 카드가 보이시죠? 이 카드는 세 자리 자연수의 각 자릿수입니다. 이 수를 제곱해 나온 여섯 자릿수(➊➋➌➍➎➏)를 두 개의 세 자릿수(➊➋➌, ➍➎➏)로 나눠 더하면 원래 수가 나와야 해요.

예를 들어 9로만 이뤄진 세 자릿수 999는 이 조건을 만족합니다. 9992=998001이고, 998+1=999니까요. 이런 수를 특별히 ‘카프리카 수’라고 합니다. 999가 아닌 다른 카프리카 수를 찾아주세요! 지금 바로 수학동아 블로그(mathdonga.blog.me) 해당 게시물에 정답을 남겨주세요. 2명을 추첨해 선물을 드립니다. 서두르세요, 어서 풀지 않으면 조혜인 기자를 구하지 못 할 수도 있어요!