d라이브러리

에피소드 2 “수학으로 노는 시간입니다. 마음껏 즐기세요!”
 

축제 이튿날 교육 컨퍼런스 두 번째 시간. 이번엔 교구를 이용한 놀이 학습 시간이다. 다소 딱딱했던 전날 분위기와는 달리, 눈앞에 펼쳐진 다양한 보드게임 때문에 장내는 화기애애했다. 컨퍼런스가 진행되는 대강당이 신나는 보드게임장으로 변신했다! 하나둘씩 자리가 채워지자 그들에게는 ‘폴리오미노를 이용해 수학 문제를 증명하라!’ 는 두 번째 미션이 주어졌다. 늘 필기구와 연습장만으로 수학 문제를 접하던 우리나라 학생들은 적잖이 당황한 눈치다. 분명 모둠을 정하고 충분히 게임을 즐긴 다음, 주어진 수학 문제를 풀라고 했건만…. 똑똑한(?) 우리나라 학생들은 컨퍼런스가 시작되자마자 게임은 해보지도 않은 채, 문제는 머리로 다 풀고 자유 시간을 만끽하고 있다. 이들이 과연 수학으로 놀 수 있을까?

“게임을 충분히 즐길 줄 알아야 사물을 수학으로 생각하는 방법을 깨달을 수 있다.”IMC 위원장인  원-샤오시엔 쑨 박사의 말이다. 게임을 이용해 수학으로 잘 놀기 위해서는 게임의 정해진 규칙을 정확하게 이해하는 것이 필수다.

이번 축제에 참가한 청소년들은 16종류의 다양한 게임을 즐기며‘수학으로 노는 법’을 함께 체험했다. 그중 가장 많은 학생들이 관심과 흥미를 가졌던 폴리오미노를 소개한다.
 

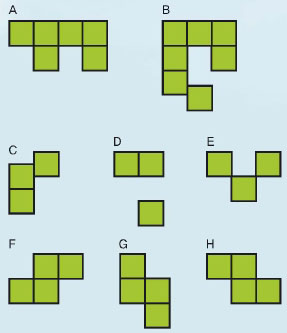
폴리오미노란 정사각형을 이어 붙여 만든 새로운 도형을 통틀어 말한다. 이때 정사각형의 변과 변이 정확히 맞닿은 것만을 폴리오미노라 한다. 만약 회전, 대칭 이동을 해 같은 모양이 되면 두 폴리오미노는 같은 것으로 간주한다. 왼쪽 그림을 살펴보자. 8개의 조각 중 폴리오미노는 몇 개일까? A와 F뿐이다. B, C, D, E는 모든 변과 변이 맞닿아 있지 않아 폴리오미노가 아니고, G와 H는 회전·대칭 이동을 하면 F와 같아진다.

폴리오미노에 대한 간단한 소개가 끝나자 학생들은 삼삼오오 모둠을 만들고 주어진 교구를 이용해 문제를 풀기 시작했다. 처음엔 학생들이 마냥 신나게 놀고 있는 건지, 정말 수학을 공부하고 있는 건지구분이 안 될 정도로 산만했다. 폴리오미노 문제를 잘 풀려면 각 폴리오미노의 조각이 회전·대칭 이동했을 때의 성질과 서로 다른 조각을 이용해 평면을 채우는 원리를 잘 알아야 한다.

그들에게 주어진 문제는 총 20문제. 문제의 난이도는 쉬운 것부터 혼자 힘으로 절대 풀 수 없는 고난도까지 다양했다. 가장 먼저 문제의 정답을 모두 맞히는 학생에겐 포상이 걸려 있었다. 이는 ‘문제를 빨리 푸는 능력’보다는‘문제를 정확히 풀기 위해 필요한 핵심 원리를 빨리 깨닫는 능력’ 을 요구하는 것이었다.

폴리오미노의 성질과 원리를 정확히 이해하려면 반드시 교구를 이용해 충분히 활동해야 했기 때문에 학생들에게 자유 시간을 준 것 이었다. 하지만 우리나라 학생들은 외국 학생들이 폴리오미노와 조금 친해졌을 무렵, 이미 문제를 다 풀어냈다. ‘문제를 빨리 푸는 능력’ 은 최고였지만, 수학으로 놀면서 자연스럽게 공부하는 것과는 거리가 멀어 보였다. 그 이유가 궁금했다. 손지현(여의도중 3년) 양에게 진짜 이유를 들을 수 있었다.“솔직히 우리나라에서는 이런 수업 시간이 초등학교 저학년 때만 주어지잖아요. 저희도 잘 놀고 즐기고 싶죠. 그런데 이미 수학을 공부하는 것과 노는 것이 머릿속에 확실히 구분돼 있는 것 같아요. 하지만 여기 와서 다른 나라 애들을 보니 학년과 나이에 상관 없이 정말 수학을 즐기고 있는 게 눈에 보여요. 여기서라도 맘껏 즐겨볼래요.”

그래도 우리나라 학생들 마음속에 꿈틀대는 열정이 보여 그나마 안심이 됐다. 우리나라 학생들도 ‘수학으로 노는 법’ 을 어려서부터 자연스레 배우는 그날을 기대해 본다.


▼관련기사를 계속 보시려면?

INTRO. 발리에서 생긴 일 세계 청소년, 수학을 즐기다!
PART 1. 수학은 언어다! 
PART 2. 수학은 놀이다!
PART 3. 수학은 집중이다!
PART 4. 수학은 흥미다!
PART 5. 수학은 참여다!