d라이브러리

안녕하세요. 수학동아에서 ‘동안’을 담당하고 있는 최 기자입니다! 오늘은 놀라운 이야기를 해드리겠습니다. 물론 제 얼굴 이야기는 아니고요, 적어도 119년 된 수학 문제가 최첨단 자율주행차 개발에 도움을 준다는 소식입니다. 대체 무슨 말이냐고요?

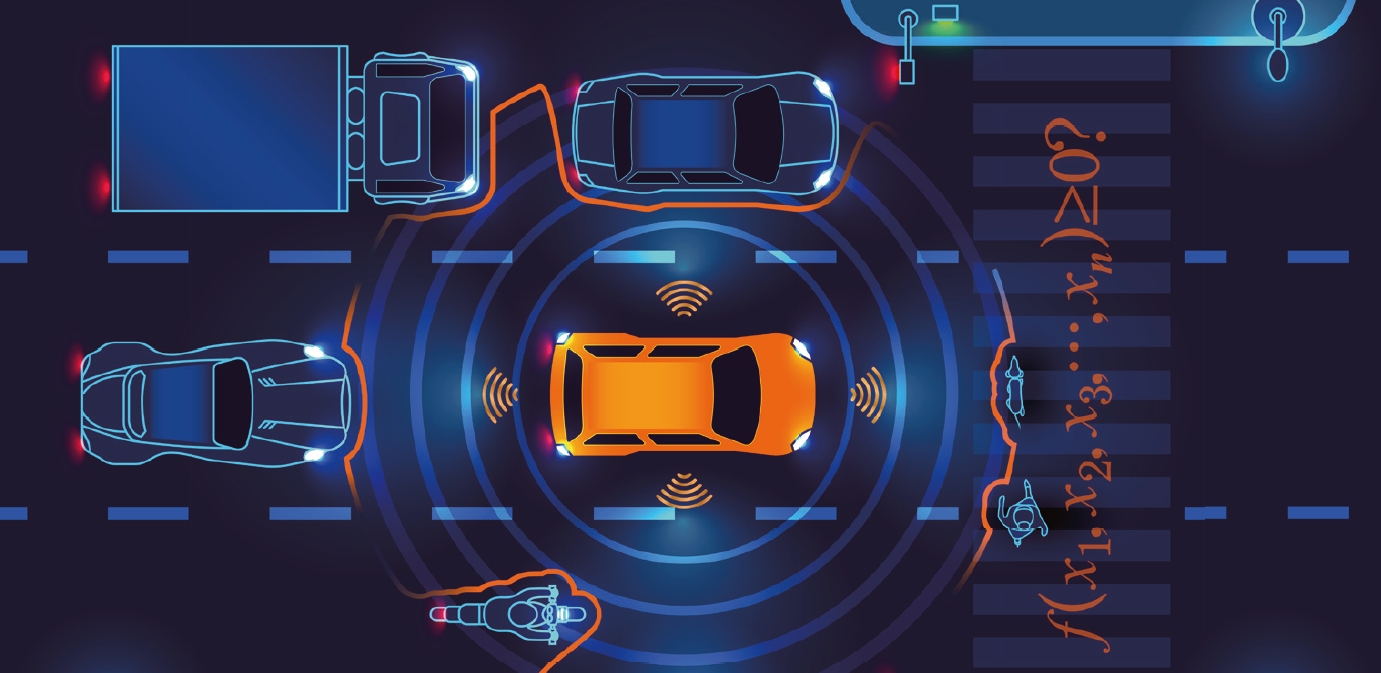
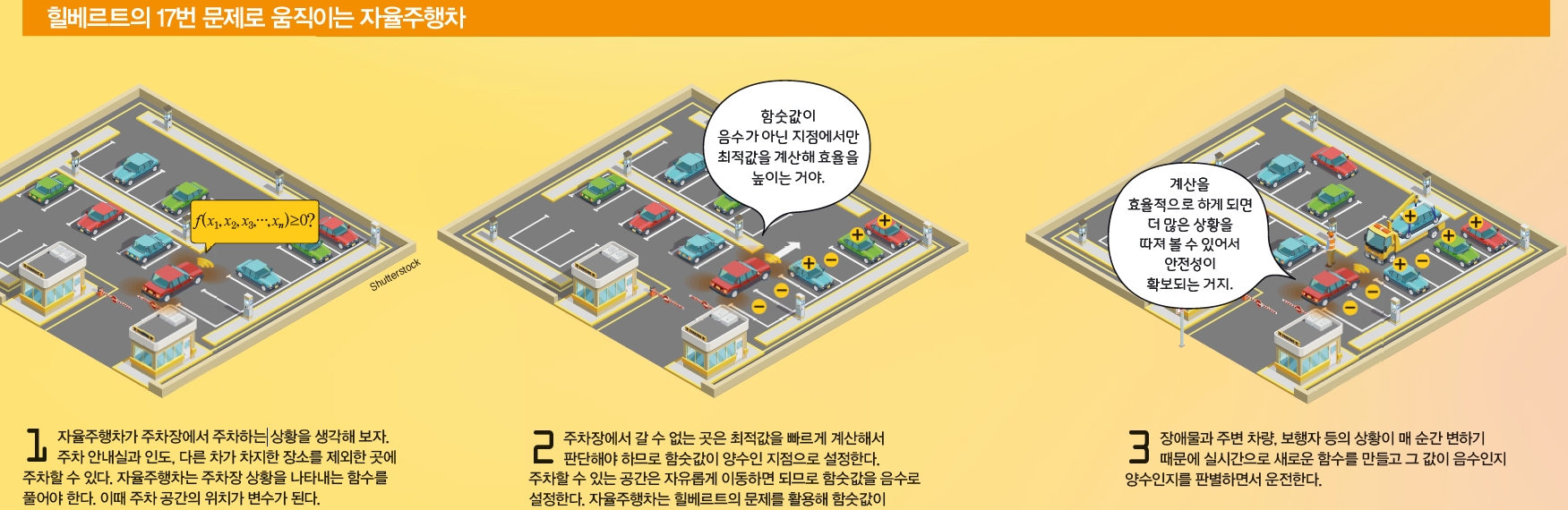
자율주행차라고 하면 무엇이 떠오르나요? 차 안에 앉은 사람이 운전대에 손을 얹지 않고 책을 읽거나 영화를 보는 장면? 맞습니다. 자율주행차는 사람이 운전하지 않고 스스로 목적지까지 요리조리 움직여 도착하는 자동차입니다.

자율주행차에서 가장 중요한 것은 당연히 빠른 시간 내에 안전하게 목적지까지 도착하는 것이죠. 자동차가 사람처럼 복잡한 도로 상황을 판단해서 스스로 운전하는 기술은 아주 어렵고 복잡해서 아직까지 완벽한 자율주행차는 나오지 못하고 있습니다.

하지만 최근 자율주행차의 성능을 지금보다 한 단계 향상시킬 수 있는 가능성이 제시됐습니다. 1900년 독일 수학자 다비트 힐베르트가 파리 세계수학자대회 기조강연에서 20세기에 꼭 풀어야 하는 문제 23개를 뽑아 발표했는데, 그 중 한 문제를 활용한 것이어서 더욱 놀랍습니다.

힐베르트의 17번 문제가 뭔데?

주인공은 아미르 알리 아흐마디 미국 프린스턴대학교 경영과학 및 금융공학과 교수 연구팀입니다. 연구팀은 힐베르트 문제 17번을 자율주행차와 로봇, 드론 등의 첨단 기계가 최적의 경로를 찾는 데 활용할 수 있다는 연구 결과를 국제학술지 ‘응용대수학및기하학’ 2019년 4월 16일자에 발표했습니다.

17번 문제는 ‘음이 아닌 유리함수를 언제나 제곱의 합 형태로 나타낼 수 있는지’를 묻는 문제입니다. 유리함수란 변수가 유리수 형태로 표현되는 함수식을 말합니다. 함숫값이 0이나 양수로만 나오면 음이 아닌 유리함수라고 말하지요. y=x²+1과 같은 이차 함수를 생각하면 이해하기 쉽습니다. 이 식에는 어떤 실수를 넣어도 1보다 큰 값이 나오죠. 이런 함수를 음이 아닌 유리함수라고 합니다.

오스트리아 수학자 에밀 아르틴은 1927년 이 추측이 참이라는 걸 증명했습니다. 예를 들어 5x²+16x+13은 (x+2)²+(2x+3)²로 다시 쓸 수 있는데, 이처럼 음이 아닌 모든 유리함수는 언제나 제곱의 합 형태로 바꿀 수 있음을 밝힌 겁니다.

하지만 잘 이해가 되지 않습니다. 음이 아닌 모든 유리함수를 언제나 제곱의 합의 꼴로 바꿀 수 있다는 게 자율주행차가 최적의 경로를 찾는 것과 무슨 상관인 걸까요?

최적값 찾아 자율주행차의 판단 돕는다

쉽게 말하면 자율주행차가 운전할 때 고려할 게 많기 때문입니다. 사람은 운전할 때 도로 상황을 보며 다양한 판단을 내립니다. 신호등은 기본이고, 주변 차선에서 움직이는 차들과 내비게이션에 나타난 이동 경로, 그리고 교통량 등을 실시간으로 고려해서 어떻게 움직일지를 판단합니다. 애초에 계획했던 경로로 가기도 하지만 상황에 따라서는 경로를 바꾸기도 하죠. 같은 방향으로 가더라도 좌우 차선에 차량이 많이 없으면 차선을 바꿉니다.

자동차가 자율주행하려면 이 모든 것을 변수로 삼은 함수를 계산해야 합니다. 쉽게 말해 변수가 여러 개인 다변수 함수를 풀어야 하죠. 함수의 최고 차수가 2차 이상일 수 있습니다. 변수 50개에 최고 차수가 10차인 엄청나게 복잡한 다항식을 풀어야 할 수도 있다는 뜻입니다. 그러려면 짧은 시간 동안 엄청나게 많은 계산을 해야 하죠.

이때 정답을 얻지는 못하더라도 최적의 해를 찾는 방법이 최적화인데요, 수학적으로 표현하면 최솟값(상황에 따라서는 최댓값)을 주는 변수의 값을 찾는 것이라고 할 수 있습니다. 하지만 변수가 많고 차수가 높은 복잡한 다항식은 정답을 구하는 것 만큼이나 어렵죠.

힐베르트의 17번 문제는 바로 여기에 도움을 줄 수 있습니다. 복잡한 다항식을 제곱의 합의 꼴로 바꾸면 전보다 쉽게 최솟값을 구할 수 있기 때문이죠. 일단 함수의 최솟값을 구하면 변수에 어떤 값을 넣었을 때 그 값이 나오는지 알아내는 건 상대적으로 쉬운 일입니다.

다항식의 부호를 빠르게 판별하는 새로운 방법

사실 여기까지는 이미 2000년 경에 다른 학자들도 알아냈습니다. 하지만 실제 자율주행차를 비롯한 최신 기술 연구에 활용할 수 없는 치명적인 문제가 있었죠. 아흐마디 교수는 미국 언론사 ‘와이어드’와의 인터뷰에서 “변수가 많은 어떤 다항식이 음이 아닌지를 판단하는 것이 매우 어렵다”라고 말했습니다.

이전까지 학자들이 다항식이 음이 아닌지를 판별하기 위해 시도했던 방법은 계산이 복잡하고 시간이 오래 걸렸습니다. 차수가 최대 6차이고 변수가 10개 안팎인 수식을 판별하기에 적당한 수준이었죠. 하지만 자율주행차나 로봇, 드론 같은 기계가 자율적으로 움직이려면 50개 이상의 변수를 가진 수식을 풀어야 하기 때문에 적합하지 않았습니다.

아흐마디 교수팀은 이 문제를 해결해 비로소 힐베르트의 17번 문제를 자율주행차와 로봇, 드론 등 첨단 기술 개발에 활용할 수 있는 길을 열었습니다. 다항식이 음인지 아닌지를 판별하기 위해 사용했던 기존 방식이 복잡한 문제를 계산하는 것이었다면, 연구팀은 상대적으로 풀기 쉬운 여러 개의 식을 연립해서 푸는 방식을 제시했습니다. 그리고 이 방식을 이용하면 훨씬 빠르게 다항식이 음이 아닌지를 판별할 수 있다는 것을 밝혔죠.

연구에 참여한 아니루다 마줌다르 프린스턴대학교 기계항공공학과 교수는 와이어드와의 인터뷰에서 “연구 결과를 휴머노이드 로봇 제어를 비롯한 다양한 분야에 실제로 적용해 봤더니 훨씬 빠르게 작동해 실용성을 확인할 수 있었다”고 밝혔습니다.

최첨단 자율주행차와 로봇 제어 기술을 한 단계 발전시키는 데 119년 전 수학자 힐베르트가 제안한 문제가 돌파구가 된다니 정말 놀랍지 않나요? 힐베르트는 23개의 문제를 제시하면서 이 문제들이 인류 문명을 발전시킬 거라고 했는데 그 말이 마치 예언처럼 들어맞았습니다. 힐베르트의 문제를 공학에서 활용할 수 있도록 장애물을 없앤 연구팀의 노력에도 박수를 보냅니다! 과연 다음엔 어떤 문제가 세상을 깜짝 놀라게 할까요?