d라이브러리

수학도 문제를 낼 때 과학 용어를 소재로 활용할 때가 많다. 수학 문제를 풀다 보면 자주 접하는 소재가 있는데, 그 중 하나가 시간과 속력, 이동거리 등 물체의 운동에 관한 것이다.

수학 교과서로 공부하다보면 위와 같은 문제를 자주 접할 수 있다. 수학은 과학 원리를 설명하는 주요 언어기 때문에 수학 문제는 이와 같이 과학에서 소재를 얻는 경우가 많다.

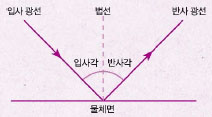
마지막으로 수학이 과학 원리를 설명하는 언어라는 점을 잘 보여 주는 사례를 소개한다. 바로 빛의 반사 법칙이다. 평평한 거울을 향해 비스듬히 광선을 발사하면 광선이 반사되는데, 이 때 입사각과 반사각은 같다.
 

그러면 빛이 포물선으로 된 면에 반사될 때를 생각해 보자. 흔히 포물선이라고 하면 그냥 불룩하게 생긴 모양을 생각한다. 하지만 포물선은 평면 위에 고정된 점(초점)과 초점을 지나지 않는 직선이 있을 때 초점과 직선으로부터 거리가 똑같은 점을 모은 곡선을 말한다.

포물선에는 여러 가지 성질이 있다. 재미있는 것은 축과 평행한 직선이 포물선에서 입사각과 반사각이 같도록 꺾이면 항상 초점을 지난다는 사실이다. 초점을 먼저 지난 직선이 포물선에서 반사되면 항상 축과 평행하게 나간다.
 

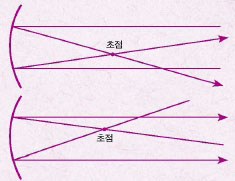
포물선의 이런 기하학적인 특성은 과학에서도 그대로 드러난다. 포물선을 이용해 만든 거울에 빛을 비추면 빛은 기하학에서 직선의 경로를 그대로 따라 움직인다. 즉, 축에 평행한 빛은 반사된 뒤 초점을 지나고, 초점을 지난 뒤 반사된 빛은 축과 평행한 방향으로 움직인다.

이런 성질은 과학 연구는 물론 우리 생활속에서도 쓰인다. 반사망원경에 쓰는 거울은 포물면, 즉 단면이 포물선이다.그래서 망원경과 평행하게 들어온 빛이 초점에 모여 선명한 상을 볼 수 있는 것이다. 전파를 수신하는 전파망원경도 마찬가지다. 넓은 포물면으로 되어 있는 전파망원경은 희미한 전파를 반사시켜 한 점에 모은다.

우리 생활에서는 자동차의 헤드라이트나 손전등이 포물선의 성질을 이용하고 있다. 헤드라이트나 손전등은 포물면과 초점에 놓인 전구로 이뤄져 있다. 초점에 있는 전구에서 나온 빛은 포물면에 반사돼 직선으로 쭉 뻗어나간다. 포물선의 기하학 원리를 이용해 사방으로 퍼지지 않고 직선으로 나가는 빛줄기를 만드는 것이다.
 

호흡이 척척 맞는 찰떡궁합으로 서로 도움을 주고받는 수학과 과학. 이 둘의 밀접한 관계는 수백 년 전부터 시작되었지만 앞으로 언제까지나 계속될 것이다. 영원한 미스터리인 자연과 수의 비밀을 밝혀 내는 찰떡콤비의 활약을 기대해 보자~!

매분 3km로 달리는 자동차가 A지점을 지나 B지점을 향해 달리고 있다. A지점을 지난 지 x분 뒤에는 A지점으로부터 ykm 떨어진 곳을 지난다고 할 때 다음 물음에 답하라.

1 x와 y사이의 관계식을 구하라.
2 A지점을 지난 지 30분 뒤에는 A지점으로부터 몇 km 떨어진 곳을 지나는가?

풀이
➊ 1분에 3km씩 움직이므로 x분 후에는 3x km 떨어진 곳을 지난다. 따라서 y=3x가 된다.
➋ y=3x에서 x에 30을 대입하면 y=3X30=90이다. 따라서 30분 뒤에는 A지점으로부터 90km 떨어진 곳을 지난다.



▼관련기사를 계속 보시려면?

영원한 찰떡궁합 수학과 과학
최초의 수학자와 과학자는 누구?
수학은 과학에 어떻게 공헌할까? ①
수학은 과학에 어떻게 공헌할까 ②
수학자? 과학자?①
수학자? 과학자?② 
과학교과서에서 찾은 수학
수학과 과학은 영원한 찰떡궁합