d라이브러리

자연을 수학이라는 객관적인 도구로 기록할 수 있게 되자 자연 현상을 공식으로 정리하는 일도 가능해졌다. 자연 현상을 법칙으로 정리할 수 있다는 말은 서로 다른 곳에서 일어나는 일도 같은 법칙으로 설명할 수 있다는 뜻이다. 예를 들어, 지구를 자전하는 달의 움직임과 날아가는 대포알의 움직임은 모두 같은 운동 법칙으로 설명할 수 있다.

또한 수학 공식으로 정리한 법칙으로 규칙성을 파악하면 앞으로 일어날 자연 현상도 예측할 수 있다. 과학의 역사에서는 이론적으로 예측한 일이 실제로 실험이나 관측 결과 사실로 드러난 사례가 많다.

✚수학으로 자손을 예측한다
 

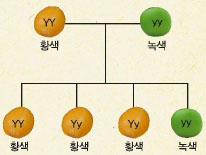
19세기 오스트리아의 식물학자인 그레고르 요한 멘델은 유전의 기본 원리를 발견했다. 정원에서 기른 여러 모양의 완두를 서로 교배한 결과 나오는 자손의 모양이 수학 원리를 따른다는 것이다.

멘델은 완두콩의 모양이 1쌍의 요소에 의해 정해지며 부모로부터 하나씩 물려받는다고 가정했다. 잡종이 되었을 때는 한쪽만 표현되는데, 표현되는 쪽을 우성, 안 되는 쪽을 열성이라고 불렀다.

이렇게 순종 황색 완두콩과 순종 녹색 완두콩을 교배했을 때 생기는 자손의 수는 2개씩 있는 요소를 각각 짝지은 경우의 수와 같다. 즉 4종류의 자손이 생긴다. 순종 황색 완두콩 하나와 순종 녹색 완두콩 하나, 그리고 잡종 완두콩 두 개다. 황색 요소가 우성이므로 잡종 완두콩 두 개는 모두 황색으로 나타난다.

따라서 서로 다른 순종 부모를 교배했을 때 생기는 자손의 모양은 우성과 열성의 비가 3:1로 나타난다. 수학을 이용하면 자손이 어떤 모양으로 나타날지 예측할 수 있다는 뜻이다.

✚보이지 않아도 찾을 수 있다

지구에서 눈으로 볼 수 있는 태양계 행성은 모두 5개다. 수성, 금성, 화성, 목성, 토성. 그보다멀리 있는 천왕성, 해왕성은 눈으로는 볼 수 없고 망원경을 이용해야 한다. 그런데 그 넓은 하늘에서 과연 어디에 있는 줄 알고 망원경을 들이대야 할까?

여기서 수학이 활약한다. 18세기에 윌리엄 허셜이 망원경으로 천왕성을 발견하고 수십 년이 지난 뒤 천왕성의 실제 궤도가 계산과 일치하지 않는다는 사실이 알려졌다. 영국의 수학자이자 천문학자인 아담스와 프랑스의 수학자 르 베리에는 천왕성 궤도에 영향을 끼치는 여덟 번째 행성이 있다고 주장했다. 그들은 각자 그 가상 행성의 궤도를 계산해 발표했다.

얼마 뒤 독일의 천문학자 갈레는 그들이 발표한 궤도를 망원경으로 관측하기 시작했다. 그리고 얼마 뒤 계산으로 알아 낸 궤도에서 얼마 떨어지지 않은 곳에서 새로운 행성을 발견했다. 태양계 여덟 번째 행성인 해왕성이었다.

지금은 행성에서 빠졌지만 명왕성 발견도 비슷했다. 곧 해왕성의 궤도가 뭔가에 의해 영향을 받는다는 사실이 드러났고, 계산에 의해 예측된 곳에서 명왕성이 발견됐다.

✚패턴에 따르는 주기율표

고대에는 물질이 몇 개의 원소로 이뤄져 있다고 생각했지만, 19세기에 이르면 발견된 원소의 수가수십 개에 이른다. 그런데 이들 원소가 일정한 규칙에 따라 배열된다는 사실을 알아 낸 사람이 있었으니, 바로 멘델레예프다.

원소를 질량에 따라 순서대로 배열하면 화학적인 성질이 주기적으로 나타난다. 멘델레예프는 이런 생각을 더욱 발전시켜 원소 주기율표를 만들었다. 잘못된 순서를 바꾸기도 했고, 주기적으로 성질이 비슷하다는 사실로부터 아직 발견되지 않은 새로운 원소의 성질을 예측하기도 했다.

훗날 화학자들은 멘델레예프가 주기율표에서 빈 공간으로 남겨 놓은 곳에 들어갈 새로운 원소를 속속 발견했으며, 성질 또한 멘델레예프의 예측과 거의 맞아떨어진다는 사실을 알아 냈다.

✚상대성이론의 예측이 사실로

아인슈타인의 상대성이론에 따르면 중력은 공간을 휘게 한다. 따라서 멀리 떨어져 있는 별에서 나온 빛은 지구로 오는 동안에 다른 별과 같은 무거운 물체 옆을 지나면서 휘어진다.

아인슈타인은 일식이 일어날 때 이 현상을 관측할 수 있으리라 예측했고, 별빛이 휘어지는 정도를 계산했다. 그리고 1919년 영국의 천문학자 아서 에딩턴은 개기일식을 관측해 태양 뒤에 있는 별에서 나오는 빛이 아인슈타인이 예측한 만큼 휘어진다는 사실을 알아 냈다.

이처럼 수학으로 예측한 사실이 훗날 실험에 의해 사실로 밝혀지는 경우는 많다. 이제 수학은 자연 현상을 정리하는 것뿐만 아니라 직접 확인하기 어려운 현상을 예측하는 데 중요한 도구다.



▼관련기사를 계속 보시려면?

영원한 찰떡궁합 수학과 과학
최초의 수학자와 과학자는 누구?
수학은 과학에 어떻게 공헌할까? ①
수학은 과학에 어떻게 공헌할까 ②
수학자? 과학자?①
수학자? 과학자?② 
과학교과서에서 찾은 수학
수학과 과학은 영원한 찰떡궁합