d라이브러리 2010년 04월 수학동아

지금까지 수학과 과학이 서로 어떤 관계인지 살펴보았다. 그러면 여기서 알 수 있는 한 가지는? 딩동댕~! 수학과 과학이 이렇게 가까운 관계라면 수학을 알면 과학을 쉽게 할 수 있다는 사실! 수학 문제에도 과학적 상황을 예로 든 게 많기 때문에 두 과목의 공통점만 잘 알아 두면 두 과목을 모두 쉽게 공부할 수 있다.

먼저 수학 개념이 과학교과서에 쓰이는 사례를 알아보자. 두 과목의 교과서에서 가장 흔히 볼 수 있는 개념 중 하나가 비례다. 수학에서는 초등학교 6학년 때 처음 비례식에 대해 배운 뒤 중학교에 들어가면 함수를 배우면서 좀 더 정확한 비례의 정의를 배운다. 비례에는 정비례와 반비례가 있다.

정비례는 두 개의 변수가 있을 때 하나의 값이 2배, 3배, 4배, …로 늘어날 때 다른 하나의 값도 똑같이 2배, 3배, 4배, …로 늘어나는 관계를 말한다.

두 변수를 각각 x와 y로 놓았을 때 정비례는 y=(어떤 수)×x와 같은 식으로 나타낼 수 있다.

수학교과서에서 이처럼 공식까지 써 가며 정확히 배운 비례 개념은 과학교과서를 공부할 때 유용하다. 중학교 1학년 때 배우는 힘과 운동 단원의 탄성력 부분을 보자. 탄성력은 용수철이나 활과 같은 물체가 힘을 받아 모양이 변했다가 원래 모양으로 되돌아가려는 힘을 말한다. 이 때 용수철에 추를 매달면 용수철이 늘어나는 길이는 매단 물체의 무게에 정비례한다. 이런 관계를 이용하면 용수철이 늘어난 길이를 측정해 매단 물체의 무게를 알아낼수 있다.

이런 관계를 보기 좋게 정리할 때 흔히 그래프를 쓰는데, 그래프도 수학과 과학에서 모두 자주 쓰는 도구다. 수학에서는 주로 함수를 좌표평면 위에 나타낸 그래프를 많이 다룬다. 과학에서는 조금 다르게 과학적인 현상을 그래프로 나타내 여러 요소의 변화와 관계를 쉽게 보여 주기 위해 그래프를 많이 쓴다. 다음 두 그래프를 보자.

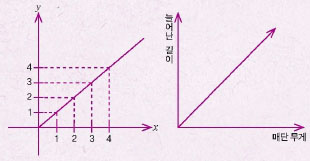
두 개의 그래프는 표현 방식이 조금 다르지만 알고 보면 똑같은 그래프다

두 개의 그래프는 표현 방식이 조금 다르지만 알고 보면 똑같은 그래프다. 수학에서는 두 변수의 관계를 함수로 엄밀히 나타낸 반면, 과학에서는 현상을 알아보기 쉽도록 단순하게 표현했을 뿐이다. x를 무게, y를늘어난 길이라고 생각하면 둘 다 무게와 늘어난 길이와의 관계를 나타낸 그래프가 된다. 이렇게 수학과 과학에는 겉보기는 조금 달라도 알고 보면 똑같은 원리가 곳곳에 있다. 그건 곧 하나만 알아도 둘을 알 수 있다는 뜻!

용수철에 매단 추의 무게가 2배, 3배, 4배, …가 되면 늘어나는 길이도 2배, 3배, 4배, …가 된다.

d라이브러리

과학교과서에서 찾은 수학