d라이브러리

중학교에서는 원과 직선이 만날 때, 직선이 원과 두 점에서 만나면 할선이고 직선이 원과 한 점에서 만나면 접선이라고 배웁니다. 즉 접선은 어떤 도형 또는 곡선과 한 점에서 만나는 직선으로 생각하게되지요.

그러면 정말 어떤 곡선과 한 점에서 만나면 접선이 될까요? 아래 세 그림은 모두 직선이 다른 도형과 한 점에서 만나는 경우입니다. 그러나 그림➊과 그림➌은 접선이지만, 그림➋는 접선이 아닙니다. 왜 그럴까요?
 

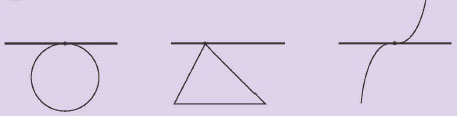
그림➋의 직선이 접선이 아닌 이유는 중학교에서 나오는 접선의 정의가 완벽하지 않기 때문입니다. 고등학교에 가면 접선은‘접점(접하는 점) 부근에서 그 도형 또는 곡선을 대신할 수 있는 직선’으로다시 배웁니다. 한 점에서 만날 뿐만 아니라 원래 도형을 대신한다는 조건도 만족해야 하는 것이죠. 아래 그림처럼 그림➊의 접점 부근을 확대하면 할수록 그림➍, ➎와 같이 원이 평평하게 보이면서 접선과 아주 비슷해 보입니다. 그런데 그림➋를 확대한 그림➏을 보면, 아무리 확대해도 접점 부근에서삼각형과 직선은 가까워지지 않습니다.
 

따라서 그림➋는 접선이 아닙니다. 즉 직선이 어떤 도형 또는 곡선과 한 점에서 만날 뿐 아니라, 접점 부근에서 도형 또는 곡선을 대신할 수 있을 때 그 직선을 접선이라고 합니다.