d라이브러리

어느 도시 지하철역에 도둑 1명이 나타났습니다. 경찰은 CCTV를 통해 도둑이 어디로 움직이는지 살피지만, 경찰 조직 내에 첩자가 있어 도둑은 CCTV가 없는 곳으로 경찰을 피해 달아납니다. 도둑과 경찰은 돌아가면서 한 번씩 이웃한 역으로 한 정거장씩 이동하는데, 자기 차례 때 움직이지 않고 그대로 있어도 상관은 없습니다. 이런 일을 반복하다가 도둑과 경찰이 같은 지하철역에 수학있게 되면 도둑은 잡히고 맙니다. 이런 상황에서 도둑을 반드시 잡으려면 경찰이 최소 몇 명이나 있어야 할까요?

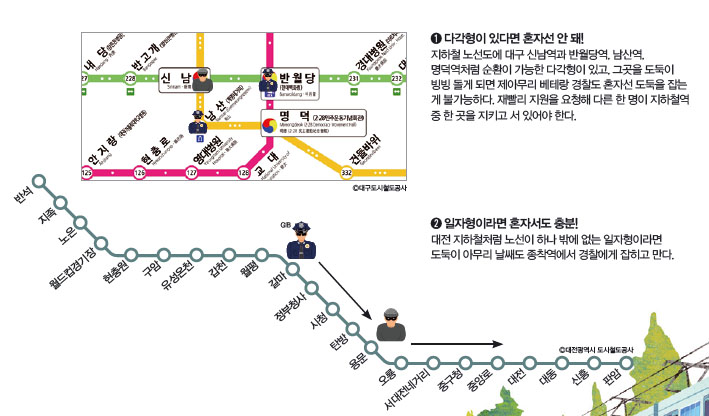
경찰 수는 지하철 노선도가 결정!
당연히 지하철 노선도의 모양에 따라 필요한 경찰의 수가 달라집니다. 예를 들어 대전처럼 지하철 노선이 하나밖에 없고 일자형이라면 도둑이 어떻게 움직이더라도 경찰 1명이 도둑을 잡을 수 있습니다. 경찰이 아무 역에서나 시작해 도둑을 쫓기만 하면 되지요. 하지만 추격전의 무대가 대구라면 경찰 1명으로는 절대 도둑을 잡을 수 없습니다.(왼쪽 노선 참고)

반월당역에서 명덕역으로, 명덕역에서 남산역으로, 남산역에서 신남역으로, 신남역에서 반월당역으로 도둑이 이동할 수 있기 때문에, 도둑이 실수하지 않는 한 도둑과 경찰은 영원히 쫓고 쫓기는 관계가 됩니다. 물론 경찰이 2명이라면 대구에서도 도둑을 잡을 수 있습니다. 경찰 1명이 수학동아반월당역에 서 있기만 하면 되지요. 그렇게 하면 남은 경찰 1명이 도둑을 쫓기만 해도 도둑이 경찰 사이에 껴서 오도 가도 못하는 상황이 펼쳐지니까요.

이 문제는 1983년 캐나다의 수학자 리처드 노바코브스키와 미국의 수학자 피터 윙클러가 연구해 논문으로 발표한 ‘경찰과 도둑 게임’입니다. 두 수학자는 경찰 1명으로 반드시 도둑을 잡을 수 있는 지하철 노선도에는 어떤 것이 있는지 밝히고, 그때 경찰의 전략을 찾아 수학적으로 증명했습니다.