d라이브러리

파도가 넘실거리는 바닷가는 여름이면 피서를 온 사람들로 북적인다. 파도는 바람에 의해 바다 표면 위의 물 입자가 가속될 때 잔물결을 일으키며 생겨난다. 파도의 움직임을 이해하려면 가장 먼저 ‘파동’에 대해 알아야 한다.

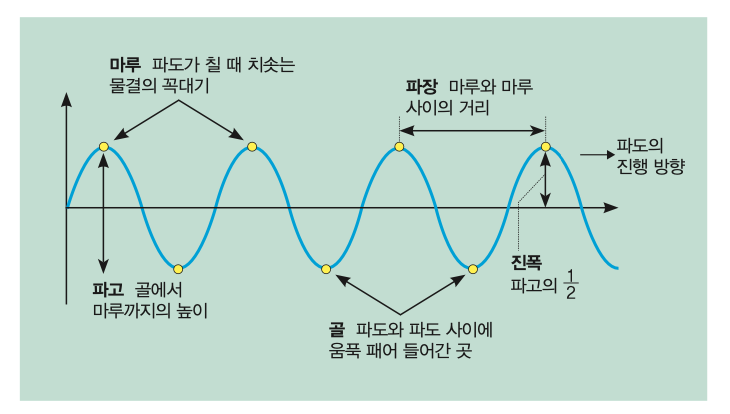
파동은 어느 한 곳에서 시작된 진동이 퍼져나가는 현상으로, 어떤 파동이든 파장, 진동수, 진폭의 3요소로 이뤄져 있다. 파장은 파동이 한 주기 동안 진행하는 거리로, 파도로 치면 마루와 마루 사이, 골과 골 사이의 거리를 말한다. 진동수는 1초 동안 진동이 일어나는 횟수로, 파도에서 1초 동안 생기는 마루의 수를 세면 된다. 이 진동수의 역수를 통해 파동이 각 지점에서 1번 진동하는 데 필요한 시간인 주기를 구할 수 있다. 마지막으로 진폭은 평균 수면에서부터의 파동의 높이로, 마루와 골의 높이 차이를 말하는 파고의 로 구할 수 있다.

파도는 파장, 진동수, 진폭 세 변수의 영향을 받아 마루와 골을 반복적으로 형성하는 ‘주기함수’다. 2차원 평면 좌표에 파도의 일부를 그리면 y = sinx와 같은 사인 곡선 그래프의 형태가 그려진다. 하지만 실제 파도는 y = sinx와 같은 한 종류의 파동만으로는 설명할 수 없다. 파도는 서로 다른 진동수를 가진 파동이 사방에서 모인 결과이기 때문이다.

 

그 대신 파도는 사인, 코사인과 같은 삼각함수 파동의 합으로 표현할 수 있다. 이렇게 복잡한 파동을 기본 파동의 합으로 나타내는 원리가 바로 ‘푸리에 급수’다. 푸리에 급수는 프랑스 수학자 조제프 푸리에가 정리한 것으로, 파동 해석, 음향학, 신호 처리, 화상 처리, 데이터 압축 등에 쓰인다.

파도의 움직임은 ‘나비에-스토크스 방정식’으로 예측할 수 있다. 나비에-스토크스 방정식은 유체의 흐름을 설명하는 비선형 편미분 방정식이다. 이 방정식의 3차원 해가 있는지 밝히는 문제는 미국 클레이수학연구소가 2000년 선정한 밀레니엄 문제 7개 중 하나로, 이를 해결하면 100만 달러(약 13억 원)의 상금을 받는다. 하지만 이 문제는 아직 풀리지 않았다. 그래서 학자들은 나비에-스토크스 방정식의 여러 근사해를 구할 수 있는 식을 개발해 해류의 흐름이나 파도의 영향을 연구하고 있다.

해변에서 수학 문제를 푼 수학자

1966 필즈상 수상자인 미국 수학자 스티븐 스메일은 일 년의 대부분을 브라질 리우데자네이루의 코파카바나 해변에서 보낸다. 바다에서 놀다 보면 안 풀리던 문제도 풀리기 때문이다. 코파카바나 해변은 4km에 이르는 흰 모래사장과 반달 모양의 해변으로 유명해 서핑하는 사람들이 많이 찾는 곳이다.
1960년 스메일은 이 해변에서 카오스 이론의 ‘혼돈계’를 쉽게 설명할 아이디어를 떠올렸다. 카오스 이론은 겉으로는 무질서해 보이지만, 그 안에 일정한 규칙이 있고, 그 속의 작은 변화가 완전히 다른 결과를 가져오는 ‘혼돈계’를 설명하는 학문이다. 그는 혼돈계를 찰흙 덩어리에 비유했다. 다양한 색이 섞인 찰흙 덩어리에 두 점이 있을 때, 찰흙을 늘렸다 반을 접는 행위를 반복하면 두 점의 거리가 확연히 달라진다. 이처럼 일정한 규칙대로 행동해도 결과에 큰 차이를 만들기 때문에, 찰흙의 비유는 혼돈계의 성질을 잘 보여준다고 할 수 있다. 혼돈계를 설명하는 모형 중 하나를 그의 이름을 딴 ‘스메일 편자’라고 하는데, 찰흙을 반으로 접을 때의 모양이 마치 말발굽처럼 보여서 이런 이름이 붙었다.