d라이브러리

꿈과 환상의 공간인 놀이공원에 도착하니 재밌는 놀이기구를 탈 생각에 설렌다. 특히 회전목마를 타고 있으면 마치 동화 속 세상에 들어온 듯하다. 

 

회전목마는 말과 마차가 커다란 원판 위에 고정돼 있고, 원판이 돌아가면서 함께 뱅글뱅글 도는 구조다. 이를 그림으로 간단히 나타내면 왼쪽 아래 동심원과 같다. 점 A(말)와 B(마차)가 반지름이 다른 원을 그리며 움직이는 형태다.

 

 

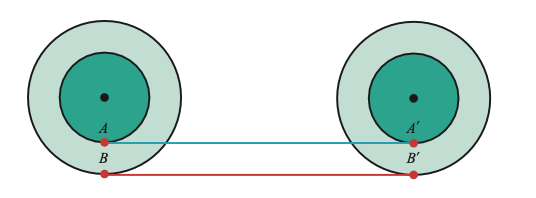
회전목마가 움직일 때 말에 타서 마차를 보면 같은 속도로 같은 시간 동안 움직이는 듯 보인다. 원주의 길이에 차이가 있으므로, 말과 마차는 결국 다른 위치에 도착할 것만 같다. 그런데 원판이 한 바퀴 돌았을 때, 이 말과 마차는 원판의 처음 위치에 와 있고 움직인 거리 또한 각각 , 로 같아 보인다. 이게 바로 고대 그리스 수학자 아리스토텔레스가 처음 발견했다고 여겨지는 ‘바퀴 역설’이다. 

 

 

 

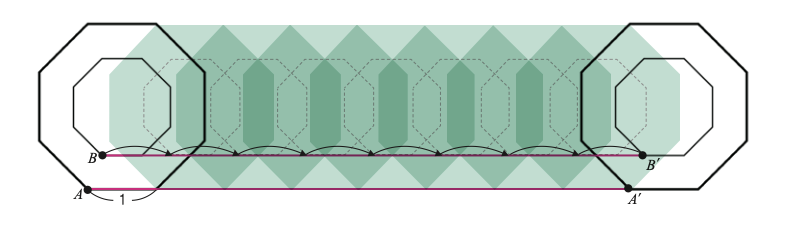
원판을 정팔각형 모양으로 바꿔 굴려보면 정확히 알 수 있다. 큰 정팔각형의 한 변의 길이를 1, 작은 정팔각형은 0.5라 하자. 이를 바퀴처럼 동시에 한 바퀴를 굴리고 나면, 큰 정팔각형의 꼭짓점 A는 A자리에 도착한다. A와 A사이의 거리는 정팔각형의 둘레인 8이다. 작은 정팔각형의 둘레는 4이므로, 이동 거리도 4가 돼야 한다. 그런데 B와 B 사이 역시 거리가 8이다.

 

이는 바퀴 속 작은 정팔각형이 건너뛰는 구간이 있기 때문이다. 큰 정팔각형은 바닥에서 미끄러지듯 구르면서, 모든 변이 바닥을 지나간다. 이때 바닥에 닿을 수 없는 작은 정팔각형은 큰 정팔각형이 구를 동안 자기 자리를 잡기 위해 위치를 건너뛴다. 즉 화살표로 표시한 것처럼 ‘건너뛰는 부분’이 생긴다.

 

정사각형은 4번, 정팔각형은 8번정n각형은 n번 건너뛴다. 정다각형의 변의 수를 무한히 늘려 원에 가까운 도형이 되면 무한개의 건너뛰는 구간이 생긴다. 이때 건너뛴 길이의 합만큼 거리 차이가 나게 된다. 이 같은 현상은 인라인스케이트와 자전거, 자동차 바퀴에서도 발견할 수 있다.

 

 

바이킹은 어떤 자리든 배에 고정돼 있어 속도가 똑같다. 하지만 끝자리가 더 무섭게 느껴진다. 그 이유는 무엇일까?

 

가장 낮은 지점과 가장 높은 지점의 높이 차이가 가운데 자리보다 끝자리에서 더 크기 때문이다. 축의 길이 r을 반지름으로 하는 부채꼴의 호가 바이킹의 배(초록색 호)라고 가정한 뒤 축의 길이(r)와 배가 상승하는 각도(α), 축과 배의 끝자리가 만드는 각도(β)를 알면 삼각비를 이용해 높이가 얼마나 차이 나는지 대략 계산할 수 있다.

 

 

파란색 보조선을 그려 계산해보자. 가운데 자리의 높이 차이는 축의 길이에서 OA의 길이 r α를 빼면 된다. 끝자리의 높이 차이는 축의 길이에서 OC의 길이  r ×cos(180° - α - β) 를 더하면 된다. 

 

만약 α가 75이고, β가 35면 끝자리의 높이 차이가 가운데 자리의 높이 차이보다 r ×(cos75° + cos70°) ≒ 0.6r만큼 더 크다.