d라이브러리

보통 두 자릿수 곱셈을 하는데 시간이 얼마나 걸리나요? 검산까지 다 해도 길어야 몇 분이죠? 만약 1경 자릿수라면요? 최근 두 수학자가 아주 큰 수를 곱하는 가장 빠른 방법을 찾았습니다.

12+23을 계산할 때 우리는 어떻게 하나요? 2+3=5를 먼저 계산하고, 1+2=3을 구해 답을 찾습니다. 즉 한 자리 숫자 덧셈을 2번 합니다. 물론 12+29처럼 받아 올림이 있는 경우는 조금 더 계산합니다. 

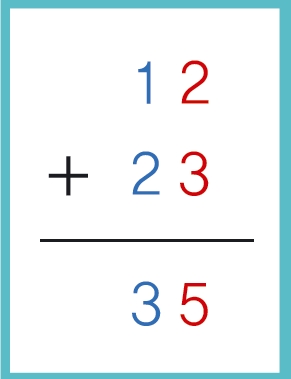
n자리 숫자의 덧셈은 어떨까요? 받아 올림을 빼고 생각하면 많아야 2n번 계산하면 됩니다. 받아 올림까지 고려해도 넉넉잡아 3n번이면 충분하죠. 

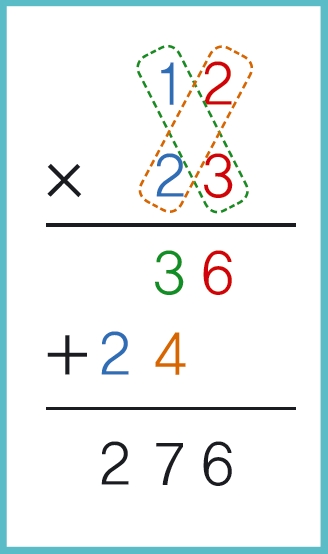
곱셈의 경우는 어떨까요? 초등학교에서 배운 그 방법, 수천 년 이상 인류가 사용해온 그 방법대로 구해봅시다. 12×23은 2×3, 1×3, 2×2, 1×2 이렇게 4번을 곱해야 합니다. 그 후 36과 240을 더해서 구하죠. 즉 이 방법대로라면 한 자릿수 곱셈을 4번 한 다음 덧셈을 해서 구할 수 있습니다. 만약 n자릿수 2개를 곱한다면 한 자릿수 곱셈을 n2번이나 하게 됩니다. 즉 이 방법으로 n자릿수 2개를 곱하는데 걸리는 시간은 n²에 비례해 늘어납니다.

자연수의 곱셈을 다항식 곱셈으로! 

더 빠른 곱셈 방법은 없을까요? 러시아의 유명한 수학자 안드레이 콜모고로프는 1960년 러시아 모스크바 국립대학교에서 열린 세미나에서 n²보다 빠른 곱셈 방법에 대해 질문했습니다. 
그런데 단 1주일 만에 당시 학생이었던 아나톨리 알렉세예비치 카라추바가 n2보다 빠른 방법을 찾았습니다. 콜모고로프는 너무 기뻐서 카라추바의 결과를 여러 곳에 알렸고, 1962년 저자를 카라추바로 한 논문을 직접 써서 러시아 과학 한림원에서 만드는 학술지에 출판했습니다. 카라추바는 한림원에서 보내온 저자용 논문 인쇄본을 보고 나서야 자기 이름으로 논문이 나온 것을 알았다고 합니다.

참고자료

데이비드 하비, 요리시 판데르후번 ‘Integer multiplication in time O(nlogn)’, 데이비드 하비, 요리시 판데르후번, 그레고이르 르세프 ‘Even faster integer multiplication’, 아나톨리 알렉세예비치 카라추바, 유리 페트로비치 오프만 ‘Multiplication of many-digital numbers by automatic computers’

ㅁㅁ