d라이브러리

여행을 떠나기 전 짐을 싸는 건 여간 귀찮은 일이 아니다. 생각나는 대로 짐을 챙기다 보면 짐이 가방에 다 들어가지 않아 난감할 때도 있다. 그런데 수많은 짐 중 어떤 것부터 골라서 싸야 하는지 알려주는 수학 이론이 있다. 바로 ‘배낭 문제’다.

배낭 문제란 넣을 수 있는 물건의 총량이 제한된 배낭에 가치의 합이 최대가 되도록 물건을 담는 조합 최적화 문제다. 이때 선택한 물건들의 무게 합은 주어진 최대 무게를 초과하면 안 된다. 배낭 문제는 단순해보이지만, 모든 경우의 수를 직접 확인해봐야 해서 답을 구하기가 어렵다.

최대 용량이 10kg인 배낭에 다음과 같은 짐을 담는 상황을 생각해보자. 배낭 문제를 통해 배낭에 담는 물건의 합이 10kg 이하가 되면서 물건 가치의 합은 최대가 되는 경우를 찾을 수 있다. 여기에는 무게순, 가치순, 무게당 가치순으로 배낭을 꾸리는 세 가지 방법이 있다.

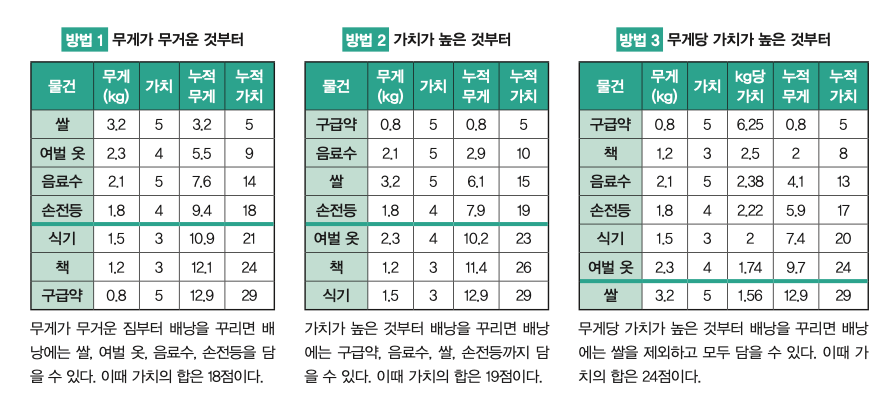
위의 세 가지 방법 중 ‘방법 3’으로 배낭을 꾸릴 때 가치의 합이 최대가 된다. 하지만 이 방법 역시 모든 물건을 넣을 수는 없다. 이는 우리가 ‘0-1 배낭 문제’를 풀었기 때문이다. 0-1 배낭 문제는 짐을 넣거나 빼거나 둘 중 하나만 선택하는 문제다. 

모든 짐을 조금씩 가져가고 싶다면 짐을 쪼개서 가져갈 수 있는 ‘분할 가능 배낭 문제’를 이용하면 된다. 0-1 배낭 문제는 이를 풀기 위한 가장 효과적인 알고리듬이 알려져 있지 않아 여러 조합을 탐색해봐야 하는 반면, 분할 가능 배낭 문제는 *그리디 알고리듬으로 해결할 수 있다.