d라이브러리

허허벌판에 길을 만들고, 나무를 심고, 곳곳에 성을 세워 점수를 얻는 타일 놓기 게임! 더 높은 점수를 얻기 위해 전략을 세우며 타일을 내려놓아요. 그런데 타일의 모양이 정사각형 아니면 정육각형이에요. 왜 그럴까요?

보드게임 타일이 될 수 있는 도형은?

타일 놓기 게임을 설계할 때 중요한 것 중 하나는 ‘타일의 모양’을 정하는 거예요. 타일을 놓을 때 타일끼리 겹치거나 빈 곳이 생겨서는 안 되기 때문에 어떤 모양으로 타일을 만들어야 그렇게 되는지 따져봐야 해요. 타일의 모양과 크기가 다 다르면 평면을 빈틈없이 채우도록 설계하는 게 어렵겠지요. 그래서 보드게임에서는 주로 한 변의 크기가 같은 정사각형이나 정육각형으로 타일을 만들어요. 정오각형이나 정십이각형 등 여러 정다각형이 있는데 왜 정사각형이나 정육각형으로만 타일을 설계하는 걸까요? 여기에 수학적인 비밀이 숨어 있어요. 

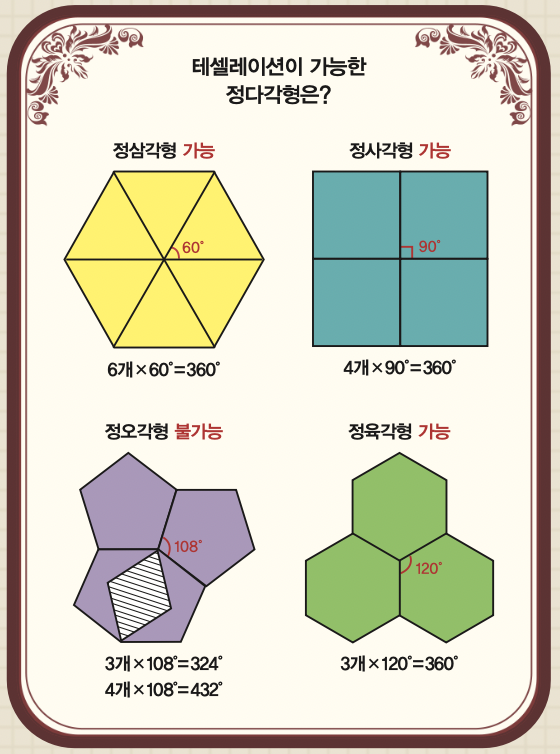
도형으로 평면이나 공간을 빈틈없이 채우는 것을 수학에서는 ‘테셀레이션’, 우리나라 말로는 ‘쪽매맞춤’이라고 해요. 수학자는 테셀레이션이 가능한 도형을 연구해요. 정다각형 중에서는 정삼각형과 정사각형, 정육각형 이렇게 세 도형만 테셀레이션이 가능하다고 알려져 있어요. 정다각형의 한 내각이 360의 약수여야만 빈틈없이 평면을 메울 수 있거든요. 

한 점을 기준으로 내각이 60인 정삼각형은 정삼각형 6개로, 90인 정사각형은 정사각형 4개로, 120인 정육각형은 정육각형 3개로 평면을 채울 수 있어요. 

반면 정오각형은 내각이 108라 한 점을 기준으로 정오각형 3개를 이어 붙이면 360에서 36만큼 모자라고, 4개를 이어붙이면 360에서 72만큼 넘쳐 빈틈이 생기거나 겹쳐지는 부분이 생기지요.

정삼각형 타일이 많지 않은 이유는?

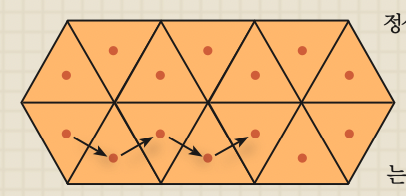
정삼각형은 테셀레이션이 가능해 보드게임 타일로 적합하지만, 타일 놓기 게임에서 정삼각형 타일을 찾는 건 쉽지 않아요. 그 이유는 정사각형이나 정육각형 타일과 비교했을 때 장점이 적기 때문이에요. 먼저 정삼각형은 한 변의 길이가 같을 때 넓이가 세 도형 중 가장 작아 게임 요소를 많이 표기하기 어려워요. 또 타일 위에서 움직이는 말의 이동이 부자연스러워요. 말은 타일의 중심을 따라 이동하는데 정사각형이나 정육각형 타일에서는 직선으로 움직일 수 있지만, 정삼각형 타일에서는 아래쪽 그림처럼 계속 지그재그로 이동해야 해요. 

정삼각형 타일을 활용하는 보드게임이 아예 없냐고요? 그렇지는 않아요. 정삼각형 타일의 장점은 여러 개를 붙여 다양한 다각형을 만들 수 있다는 거예요. 칠교놀이처럼 타일 조각을 이용해 여러 도형을 만드는 보드게임에 활용되고 있어요.

<;개발자 노트>;

정육각형 타일을 조합하라!

안녕하세요. 보드게임 ‘더스트 플래닛’을 개발한 염지현 작가예요. 더스트 플래닛은 미세먼지 괴물의 습격으로 황폐화된 땅에 숲과 초원, 습지, 연구소 타일을 올려 동물이 살 수 있는 터전으로 바꾸는 게임이에요. 

게임의 핵심 요소인 타일을 어떤 모양으로 만들지 고민한 끝에 다양한 전술을 세울 수 있는 정육각형 타일을 쓰기로 했어요. 그런 다음 정육각형 타일을 게임판에 배치했지요. 그런데 타일 위에 말을 놓을 때마다 타일들이 쉽게 흩어지는 단점이 있었어요. 그래서 ‘폴리오미노’를 떠올리면서 과감하게 정육각형 타일들을 이어 붙였어요. 폴리오미노는 크기가 같은 정사각형 여러 개를 변이 맞닿게 붙여 하나로 이어 만든 평면도형이에요. 

저는 먼저 정육각형 서너 개를 변끼리 맞닿게 이어붙여 만들 수 있는 타일 모양을 모두 그려놓은 다음, 게임 진행에 방해되는 타일을 제외했어요. 예를 들어 정육각형 4개를 일렬로 이어붙인 ‘ㅡ자형’ 타일은 내려놓을 때마다 게임판을 크게 가로질러 다음 타일을 놓기 어려웠어요. 그래서 최종 구성에서 뺐지요. 

여러 번의 테스트를 반복해 정육각형 세 개 또는 네 개를 이어 붙인 조각 타일 6종류를 만들고, 카드 게임의 조커 같은 역할을 할 정육각형 1개로 만든 타일을 추가했어요. 이렇게 모두 7가지의 정육각형 타일을 완성했답니다. 평소 퍼즐 속 수학 원리를 즐겨 분석해 왔던 내공 덕분에 보드게임을 무사히 완성할 수 있었어요.