아침밥을 먹는 학생과 먹지 않는 학생의 고득점할 확률을 비교할 때 왜 퍼센트(%)로 이야기하는 걸까? 정확하게 그 수가 몇 명인지 궁금한데 그건 알려주지 않고 말이다.
퍼센트는 객관적인 정보를 근거로 다른 사람을 설득하는 글에서 수치를 나타내기 위해 자주 쓴다. 그러나 수치를 써서 사실을 감추고, 쓰는 사람의 입맛대로 주장을 펼칠 수 있어 퍼센트가 등장하는 글은 내용을 꼼꼼하게 따져봐야 한다. 먼저 왜 퍼센트를 쓰는지부터 살펴보자.
아침밥을 먹는 학생과 먹지 않는 학생의 성적을 비교하는 실험을 한다고 생각해보자. 실험 기간 중 아침밥을 먹지 않는 학생 1,000명 가운데 성적이 오른 학생은 5명이다. 반면 아침밥을 먹는 학생 1,000명 가운데 성적이 오른 학생은 6명이다. 이 실험 결과를 세 가지 방법으로 나타낼 수 있다.
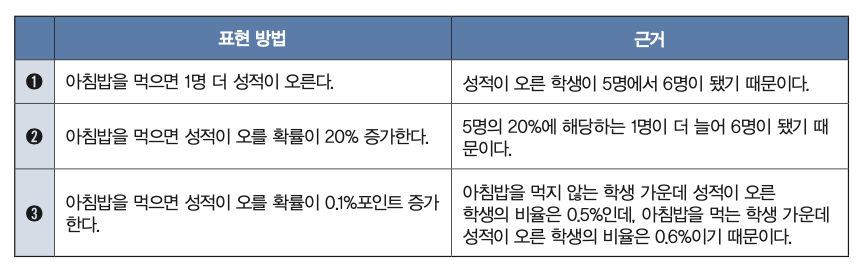
표현 방법 : 아침밥을 먹으면 1명 더 성적이 오른다.
근거 : 성적이 오른 학생이 5명에서 6명이 됐기 떄문이다.
2.
표현 방법 : 아침밥을 먹으면 성적이 오를 확률이 20% 증가한다.
근거 : 5명의 20%에 해당하는 1명이 더 늘어 6명이 됐기 떄문이다.
3.
표현 방법 : 아침을 먹으면 성적이 오를 확률이 0.1%포인트 증가한다.
근거 : 아침밥을 먹지 않는 학생 가운데 성적이 오른 학생의 비율은 0.5%인데, 아침밥을 먹는 학생 가운데 성적이 오른 학생의 비율은 0.6%이기 때문이다.
아침밥을 먹는지를 기준으로 성적이 바뀐 정도를 나타내는 수치는 1명, 20%, 0.1%포인트 이렇게 세가지로 나타낼 수 있다. 이 가운데 가장 눈에 띄는 수치는 20%다. 일단 가장 크기 때문이다. 학생에게 아침밥을 먹는 습관을 적극적으로 권장하기 위해서는 ‘❷ 아침밥을 먹으면 성적이 오를 확률이 20% 증가한다’라고 홍보하는 것이 가장 효과적이다.
반대로 아침밥을 먹지 않아도 된다고 주장하고 싶다면 ‘1명만 성적이 올라’, ‘0.1%포인트 증가에 그쳐’라는 표현을 쓴다. 글에는 이렇게 글쓴이의 의도가 반영된다.
반값 할인, 반값 증가?
‘50% 할인’ 문구를 보고 마트로 한달음에 달려간 적이 있을 것이다. 50% 할인은 ‘원래 가격의 50%만큼 가격을 낮춘다’라는 뜻이다. 1만 원짜리 화장품도 5,000원에 살 수 있고, 3,000원짜리 과자는 1,500원에 살 수 있다. 그렇다면 할인 기간이 끝나고 1,500원짜리 과자를 도로 3,000원에 파는 경우에도 ‘가격이 50% 증가한다’라고 할까?
이때는 ‘가격이 100% 증가한다’라고 한다. 3,000원짜리 과자를 1,500원에 팔 때는 3,000원의 50%에 해당하는 1,500원을 깎았기 때문에 ‘가격이 50% 감소’라고 할 수 있지만, 1,500원에 팔던 과자를 3,000원에 팔 때는 1,500원의 100%에 해당하는 1,500원을 더 받기 때문에 ‘가격이 100% 증가’라고 표현해야 한다.
또 다른 예를 살펴보자. 다음 기사에는 어떤 오류가 있을까?
도로사고 연평균 5% 증가
2022년 우리 지역의 교통사고는 전년도인 2021년보다 60% 증가했다. 그렇지만 2023년에는 전년도인 2022년보다 50% 감소했다. 2년 간 10% 증가했으므로 연평균 5% 증가한 꼴이다.
인구 1,000명을 기준으로 교통사고 건수가 2021년에 10건, 2022년에 16건, 2023년에 8건 일어났다고 하면 2022년 교통사고 건수는 전년도의 60%에 해당하는 6건만큼 늘었다. 따라서 기사 속 ‘60% 증가’라는 표현은 맞는다. 반면 2023년에는 전년도 건수의 절반에 해당하는 건수만큼 사고가 났다. 즉 ‘50% 감소’도 맞는다. 그렇다면 무엇이 오류일까?
2021년과 2023년의 교통사고 건수에 집중해보자. 교통사고는 10건에서 8건으로 줄었다. 따라서 ‘연평균 5% 증가’라는 표현은 옳지 않다. 퍼센트만 봐서는 사고가 줄어들었다는 것을 알기 어려운 셈이다. 그러므로 기사를 비판적으로 읽기 위해서는 퍼센트를 이용한 의도가 무엇일지 생각해야 한다.