
실수의 한 구간, 예컨대 0 이상 1 미만인 실수는 무한히 많다. 문제는 실수를 셀 수 있느냐인데, 아무도 실수가 무엇인지 정의를 내리지 못했다. 자연수의 집합은 ‘1부터 시작해서 1씩 커지는 수로 이뤄져 있다’고 정의하지만, 0 바로 다음에 오는 실수가 무엇인지는 도무지 알 수 없었다.
실수의 정체를 밝힐 아이디어는 독일의 수학자 리하르트 데데킨트에게서 나왔다. 아이디어의 이름은 ‘데데킨트의 절단’. 그는 ‘유리수 전체를 크기 순서대로 나열한 수직선’을 자르는 사고 실험을 했다. 잘린 수직선 두 개 가운데 작은 수가 있는 쪽을 집합 A, 큰 수가 있는 쪽을 집합 B라고 하면 아래와 같이 네 가지 경우의 수를 생각할 수 있다.
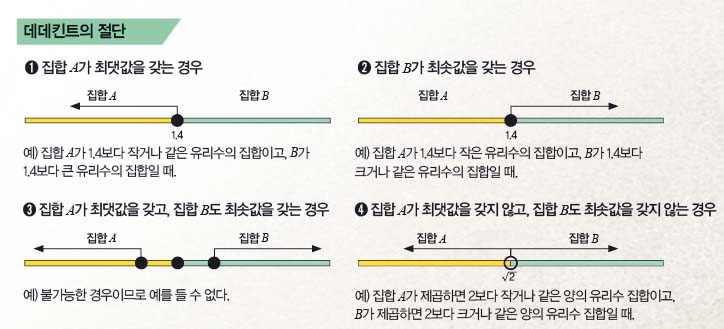
절단 결과, ➌은 일어나지 않는다. 그런 경우가 생겼다면 잘린 부분 근처에 A의 최댓값보다는 크고 B의 최솟값보다는 작은 유리수가 있을 것이다. 그러나 이 유리수는 수직선 위의 유리수 중 하나로서 A 또는 B에 속할 수밖에 없어서 모순이다.
반면 ➍의 경우, 왼쪽 조각에도 최댓값이 없고 오른쪽 조각에도 최솟값이 없다. 따라서 두 조각 사이에는 분명히 빈틈이 있다! 데데킨트는 빈틈을 유리수와 다른 수로 채워 넣으면 실수의 수직선을 만들 수 있다고 했다. 여기서 빈틈을 채우는 수가 바로 ‘무리수’다. 실수는 유리수와 유리수보다 더 많은 무리수로 이뤄진 빈틈없는 수 체계다.
실수, 많아도 너무 많아!
데데킨트가 유리수와 무리수로 이뤄진 실수의 정체를 파악하고 줄을 세웠다면, 칸토어는 손님의 규모를 호텔의 규모와 비교했다. 그러나 실수를 세는 방법은 없다. 과연 칸토어가 자연수 집합과 실수 집합의 크기를 비교한 방법은 무엇이 었을까? 칸토어는 0과 1 사이의 모든 실수를 자연수와 하나씩 짝지었다고 가정하고 시작했다.
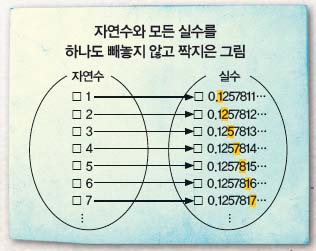
그 다음, 이 목록에 없는 실수를 찾을 수 있는지 실험했다. 먼저 왼쪽 그림과 같이 자연수 n을 배정받은 실수의 소수점 아래 n번째 자릿수를 찾아 표시해 보자. 그러면 대각선을 따라 0.1257817…이 된다. 이제 이 수의 소수점 아래 수를 모두 원래 수와 다른 수로 바꿔 새 실수를 만들어 보자. 1은 6으로, 2는 3으로, 5는 8로 바꾸는 식이다. 그림에서 생략한 자릿수도 같은 방식으로 모두 바꾼다.
그렇게 만든 실수 0.6382336…은 몇 번째 실수와 비교해도 언제나 소수점 아래 n번째 자릿수가 다르다. 즉, 실수 0.6382336…는 이 목록에 없는 수다. 칸토어는 이런 식으로 언제나 자연수와 짝지어지지 못한 실수를 찾을 수 있음을 증명했다. 따라서, 실수는 자연수보다도 더 많고 무한호텔에 방이 무한히 많아도 투숙할 수 없다.

▼관련기사를 계속 보시려면?











