d라이브러리

사리안또, 오늘은 본격적으로 글자가 어떻게 만들어지는지 알려 주려고 해. 영어와 다르게 한글은 자음과 모음을 번갈아 쓰면서 하나의 글자를 만들어. 초성(자음)과 중성(모음)으로 한 글자를 만드는 이분법과, 초성(자음)과 중성(모음), 그리고 종성(자음)으로 한글자를 만드는 삼분법 두 가지가 있지.

 한글은 자음과 모음 24개로 아주 많은 글자를 만드는 데, 간단한 곱셈으로 그 개수를 구할 수 있어. 그리고 한글 자음은 14개지만 같은 자음을 겹쳐 쓰는 겹자음과 서로 다른 자음을 써 받침에만 쓰는 받침 겹자음이 있어. 또 모음에는 두 개의 모음을 합해서 쓰는 이중모음도 있지. 한글로 글자를 만들 때는 기본 자음과 모음 말고도 겹자음, 이중모음 등 다양한 자음과 모음이 쓰이는 거야.
 

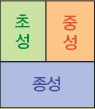
A = {ㄱ, ㄴ, ㄷ, ㄹ, ㅁ, ㅂ, ㅅ, ㅇ, ㅈ, ㅊ, ㅋ, ㅌ, ㅍ, ㅎ} , n(A) = 14
B = {ㄲ, ㄸ, ㅃ, ㅆ, ㅉ} , n(B) = 5
C = {ㄳ, ㄵ, ㄶ, ㄺ, ㄻ, ㄼ, ㄽ, ㄾ, ㄿ, ㅀ, ㅄ} , n(C) = 11
D = {ㅏ,ㅑ, ㅓ, ㅕ, ㅗ, ㅛ, ㅜ, ㅠ, ㅡ, l} , n(D) = 10
E = {ㅐ, ㅒ, ㅔ, ㅖ, ㅘ, ㅙ, ㅚ, ㅝ, ㅞ, ㅟ, ㅢ} , n(E) = 11

 집합 A는 자음 하나로 이뤄진 집합, B는 같은 자음이 두 개로 이뤄진 집합, C는 서로 다른 자음으로 이뤄진 받침집합, D는 하나의 모음으로 이뤄진 집합, E는 서로 다른 모음 두 개로 이뤄진 집합이다. 그리고 집합 A의 원소 개수를 n(A)로 표시한다.


 초성에 올 수 있는 자음은 집합 A와 B야. n(A) + n(B) = 19개가 되지. 중성에는 모든 모음이 올 수 있으니까 모음 집합인 D와 E가돼. n(D) + n(E) = 21개야. 그리고 종성에는 집합 A와 집합 C의 받침 자음이 모두 올 수 있고, 집합 B에서는 ㄲ, ㅆ 두 가지만 골라서 써.

 따라서 받침 개수는 n(A) + n({ㄲ, ㅆ}) + n(C) = 14 + 2 + 11 = 27개가 돼. 그런데 받침이 없는 경우도 있기 때문에 종성에 올 수 있는 받침 경우의 수는 27에서 1을 더해야 해.

 이렇게 계산한 초성과 중성, 그리고 종성에 올 수 있는 경우의 수를 모두 곱하면 19×21×28 = 1만 1172개가 되지. 조합으로 무려 1만 1172개의 글자를 만들 수 있어.

 그렇지만 1만 1172가지 글자가 모두 다른 소리를 내는 건 아냐. 우선 글자를 만들 때는 종성에 27가지 받침이 올 수 있지만 소리를 내는 자음은 ㄱ, ㄴ, ㄷ, ㄹ, ㅁ, ㅂ, ㅇ 으로 7가지밖에 없거든. ‘갔, 갓, 갇’이 ‘갇’으로 한 소리를 내듯이 모양은 다르지만 같은 소리를 내는 글자가 있기 때문이야.

 또 초성 중에 중성에서 서로 다른 모음을 만나지만 같은 소리를 내게 하는 자음이 있어. 자음 ㅈ,ㅊ,ㅉ는 ㅑ, ㅒ, ㅕ, ㅖ, ㅛ, ㅠ와 글자를 만들 때 ㅏ, ㅐ, ㅓ, ㅔ, ㅗ, ㅜ 모음으로 소리가 나. 이런 경우에 속하는 글자의 수는 3×6×8=144개가 돼. 여기에 ㅇ을 제외한 자음과 모음 ㅢ로 만든 글자는 소리가 ㅣ로 나므로 18×1×8=144개도 빼야 해.

 따라서 한글로 만들 수 있는 소리 개수는 19×21×8=3192에서 144를 두 번 뺀 2904개야. 만약 사라진 자음과 모음 4개가 더 있었다면 글자와 소리는 이보다 더 많았겠지.
 

p.s)

원래 세종대왕이 처음으로 한글을 만들 때는 17개의 자음과 11개의 모음으로 지금보다 4개가 더 많았어. 모음 하나(•)와 자음 3개(ㅿ,ㆆ,ㆁ)가 더 있었지. 모음 중에서도 기본이 되는 ‘•(아래 아)’는 한글이 만들어질 때 가장 중요한 역할을 했어. 그리고 자음 ㅿ은 여린 시옷으로 ㅇ과 ㅅ의 중간음을, ㆆ은 목구멍에서 나는 소리로 ㅎ보다 깊고 ㅇ보다 얕은 소리, 그리고 ㆁ은 여린 기역으로 목구멍과 혀 사이의 소리를 내.



▼관련기사를 계속 보시려면?

수학을 닮은 한글 
첫 번째 대칭과 회전으로 만든 한글
두 번째 조합으로 만든 한글 글자는 몇 개일까?
한글은 디지털에도 안성맞춤
세 번째 한글 자음 'ㅇ'은 숫자 0과 비슷해 
수학자의 꿈, 필즈상 수상자를 만나다 
최고 수학자는 누구?
필즈상 수상자와의 만남 
한국 수학의 밤