d라이브러리

무한에 대한 힐베르트의 설명을 듣고 창의적인 발상에 놀랐소? 하지만 아직 이르오. 난 무한의 크기를 비교할 수 있는 기술을 만들어냈으니까 말이오. 이 기술로 무한 세계를 손바닥의 손금 보듯 샅샅이 살펴볼 수 있소!

자연수의 무한집합이 클까요, 짝수의 무한집합이 클까요? 답은 ‘크기가 같다’입니다. 짝수는 자연수에서 홀수를 뺀 나머지이니, 자연수 집합 크기의 반이라고 생각할 수 있어요. 하지만 자연수와 짝수를 하나하나 짝지을 수 있어서 두 집합의 크기는 같습니다.

자연수 1을 짝수 2, 자연수 2를 짝수 4와 연결해 보세요. 이같이 자연수에 2를 곱한 짝수들과 연결하면 자연수와 짝수 사이에 ‘일대일 대응’이 만들어지겠죠? 짝수뿐만 아니라 홀수, 정수, 유리수 역시 자연수와 일대일 대응이 가능하므로 모두 크기가 같으며, 이런 집합을 ‘셀 수 있는 무한집합’이라고 합니다.

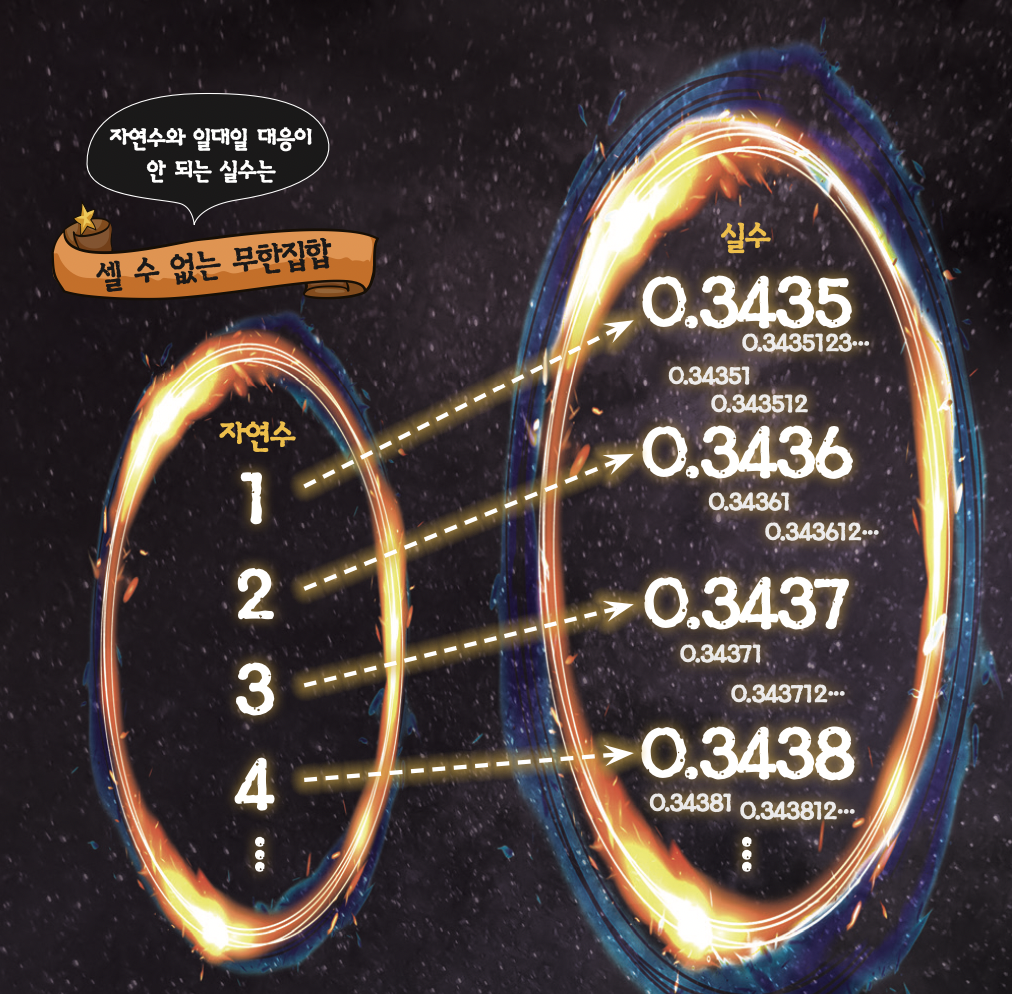
실수도 자연수와 크기가 같을까요? 실수는 자연수와 일대일 대응할 수 없습니다. 예를 들어 실수 중 0.3435를 골라 1과 대응시키고, 0.3436은 2, 0.3437은 3과 대응시키면 겉으로는 일대일 대응이 되는 듯 보입니다. 하지만 0.3435와 0.3436 사이에는등 자연수의 개수보다 많은 실수가 존재하기 때문에, 일대일 대응이 되지 않습니다.

따라서 실수나 무리수의 경우에는 자연수와 일대일 대응이 되지 않아 집합의 크기를 가늠할 수 없는 ‘셀 수 없는 무한집합’이라고 합니다. 칸토어는 일대일 대응을 이용해 실수 집합의 크기가 자연수 집합 보다 항상 크다는 것을 증명했습니다.