d라이브러리

으아~. 정말 답답하네. 역사적 기록에도 독도는 우리땅이고, 현재 독도에서 사는 사람들도 대한민국 국민이잖아. 그런데 왜 우기는 거야~. 명쾌한 증명이 필요하겠는걸? 예를 들면 수학으로 증명하는 거지!

일본의 독도연구가 가와카미 겐조는 1966년 독도가 일본 땅이라는 논리를 펴기 위해 ‘다케시마의 역사지리학적 연구’라는 책을 완성했습니다. 그 책의 제 3장에는 수학적 분석을 통해 울릉도와 독도 간 가시거리를 측정했어요. 그리고 겐조는 “울릉도의 어느 높이에서도 독도를 육안으로 식별할 수 없다”며 “한국인은 독도의 존재 자체를 인지하지 못했다”고 주장했습니다. 앞서 1454년 세종실록지리지에 울릉도에서 독도가 보인다는 기록을 반박하는 내용이었죠. 이후 이 주장은 오랫동안 한국보다 일본이 독도를 먼저 발견했다는 주장의 근거로 쓰였습니다.

그러던 2009년 당시 서울 용산세무서장이었던 정태만 인하대학교 고조선연구소 교수는 ‘독도 문제의 수학적 접근’이라는 논문을 발표하고 겐조가 펼친 주장이 허술하다고 반박했어요. 이때 사용된 수학 개념은 삼각함수와 피타고라스 정리로 꽤 간단한 수학식으로 오랫동안 사실처럼 주장해온 겐조의 주장을 반박한 거죠. 그렇다면 정 교수는 어떤 방법으로 독도가 우리땅임을 증명했을까요?

수학으로 봐도 독도는 우리땅!

지구는 둥글기 때문에 지구 반대편의 나라는 볼 수 없습니다. 울릉도와 독도 역시 서로 멀리 떨어져 있으면 보이지 않을 수도 있겠죠. 정말 그럴지 수학으로 계산해봅시다.

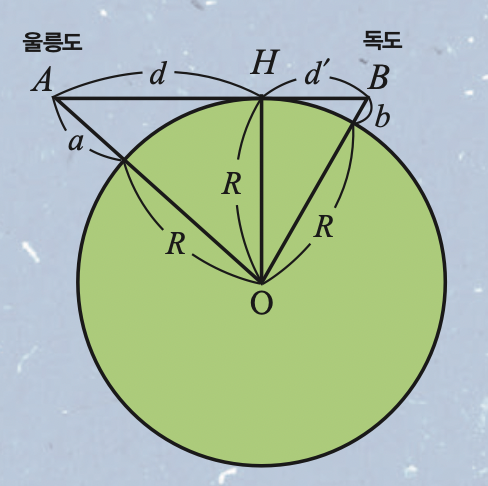
먼저 지구처럼 동그란 원 위에 독도(B)를 그립니다. 이때 b는 독도의 높이입니다. 울릉도에서 독도의 꼭대기가 보이는 높이를 찾기 위해 B에서 수평선 H까지 직선을 긋고 울릉도와 만나는 지점을 A라 둡니다. 그리고 선분 AH 거리를 d,  선분 BH 거리를 d' 라 합시다. 여기서 △OHB에 피타고라스 정리를 적용하면 (R+b)²=R²+d'²이고 이를 d' 에 대해 정리하면 d'= √ (2Rb+b²)가 됩니다. 이 식에서 독도 높이의 제곱인 b²은 지구 반지름 R에 비해 매우 작은 값이고, 매우 큰 수 2Rb에 더해도 계산에 큰 영향을 주지 않기 때문에 무시합니다. 그럼 d'≒ √ (2Rb)= √ (2R)+ √ b라 생각할 수 있죠. 같은 방식으로 d를 계산하면 d≒√ (2Ra)= √ (2R)+ √ a가 됩니다.

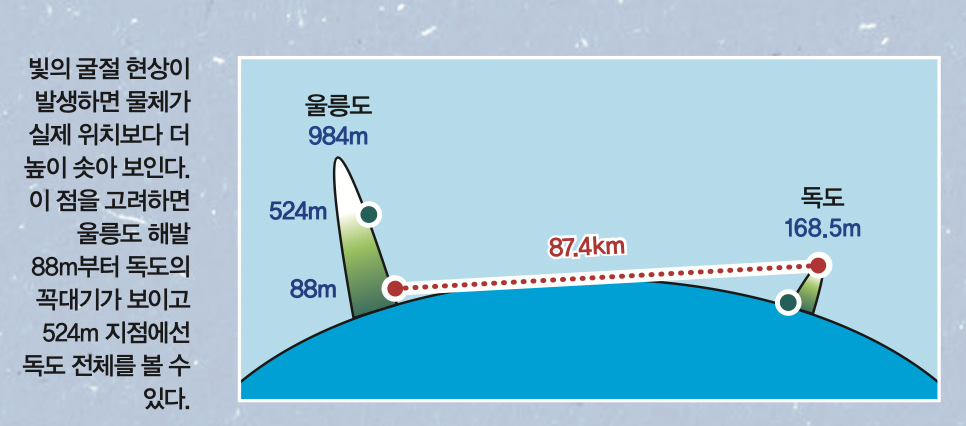
이제 실제 값을 대입해 울릉도에서 독도를 볼 수 있는지 계산해볼까요? 울릉도와 독도의 거리는 d'+d= √ (2R)× √ a+√ (2R)× √ b로 나타낼 수 있습니다. 이때 지구 반지름 R에 6378.137km를, 울릉도와 독도의 거리(d+d')에는 간조 시 해안선의 최단거리인 87.4km를, 독도의 높이(b)에는 168.5m를 대입해줍니다. 그럼 독도를 볼 수 있는 울릉도의 높이 a는 약 132.02m가 나오죠. 울릉도에서 가장 높은 곳의 높이가 984m이기 때문에 울릉도에서 충분히 독도를 볼 수 있습니다. 정 교수는 “빛 반사로 인한 오차, 간조와 만조 시기의 울릉도와 독도의 높이 변화, 그리고 더 높은 곳으로 올라갈수록 두 섬의 거리가 멀어지는 것들까지 계산하면 울릉도의 해발 88m부터 독도가 보이기 시작해 524m에 오르면 독도 전부를 볼 수 있다”고 증명했습니다. 실제로 권오철 천체사진작가는 위와 같은 방법으로 울릉도에서 독도가 잘 보이는 높이를 구해 울릉도에서 독도를 촬영할 수 있었답니다.