d라이브러리

  ◼︎   그리스어 연습장   ◼︎

19세기 말 영국. 한 소년이 의자에 앉아 일기를 쓰고 있습니다.

그런데 일기장의 표지엔 ‘그리스어 연습장’이라고 적혀 있네요. 자신의 생각이 집안 어른들에게 들키지 않기를 바란 소년이 써놓은 위장 제목이었습니다. 첫 장을 이 일기로 시작하는 그리스어 연습장에는 신의 권능, 자유 의지, 도덕, 영생, 이성과 감성에 관한 청소년 버트런드 러셀의 성찰이 기록돼 있습니다.

게다가 그리스어 알파벳을 이용해 일기를 썼어요. 그리스어 알파벳을 같은 소리의 로마어 알파벳으로 바꾸면 뜻을 알게끔 한 것이지요. 이런 암호까지 이용해서 일기를 썼다는 것은 소년이 매우 민감하고 혼란스러운 시기를 거치고 있다는 뜻이 아닐까요? 무엇이 소년의 마음을 그토록 불편하게 만든 걸까요?

◼︎   신앙심이 흔들리다  ◼︎   

원뿔 모양의 산에 집 A와 B가 있습니다. 두 집을 잇는 가장 짧은 경로는 무엇일까요? 이 문제를 주변 사람에게 내면 열에 아홉은 산 둘레를 두르는 붉은색 경로가 가장 짧다고 답합니다. 직관적으로 이것은 당연해 보입니다. 산 위를 거치는 경로는 오른 경사만큼의 거리를 더 이동해야 하니까요.

그러나 두 집을 잇는 가장 짧은 것은 파란색 경로입니다. A에서 B까지 가는 최단 경로를 구하기 위해서 원뿔의 전개도를 펼쳐봅시다. 전개도를 펼치면 파란색 경로는 직선, 붉은색 경로는 곡선이므로 최단 경로는 파란색 경로임을 엄밀하게 증명할 수 있습니다.

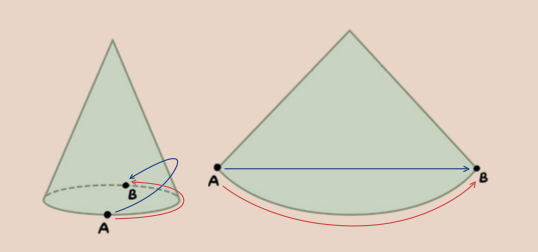
이 이야기를 꺼낸 이유는 ‘당연해 보이는데?’라는 직관이 수학에서 얼마나 위험한지 보여주기 위해서입니다. 수학의 세계에서 참과 거짓의 여부를 결정하는 판사는 직관이 아니라 ‘이성’입니다. 오직 명증하고 엄밀한 논리를 통해 다다른 결론만이 수학적으로 인정받을 수 있습니다.

3

어렸을 때부터 유클리드 기하학을 배운 러셀은 검증되지 않은 것의 위험과 명증하고 엄밀한 논리의 중요성을 잘 알고 있었습니다. 문제는 이러한 러셀의 가치관이 가정환경과 충돌하면서 시작됐지요. 러셀의 할머니는 독실한 기독교인이었습니다. 러셀은 할머니의 영향으로 신앙심을 갖고 있었지만, 한편으로는 신을 의심했습니다.

사춘기에 접어들며 수학으로 갈고 닦인 러셀의 예리한 사고 능력이 할머니의 종교관을 향하기 시작했습니다. 러셀은 유클리드 기하학을 배우며 ‘평행선 공준’마저 의심한 소년입니다. 그런 소년에게 신이 세계를 7일 만에 창조했고, 자신의 형상을 본떠 아담을 만들었으며, 십자가에 못 박힌 예수가 3일 후에 부활했다는 이야기가 어떻게 안 의심스러울 수 있었을까요? 그러나 기독교 신앙을 배척한다는 것은 러셀에게 가정에서의 완전한 고립과 정체성의 상실을 의미했습니다.

불편한 마음을 해결하고자 러셀은 우화 ‘임금님 귀는 당나귀 귀’의 이발사가 그랬듯이 어떻게든 자기 생각을 정리하고 표출하기 위해 그리스어 연습장으로 위장한 철학 일기를 쓰기 시작했던 겁니다.

어느덧 러셀은 언덕 너머로 저무는 석양에 감탄하던 어린아이에서 날카로운 수학적, 철학적 사고로 무장한 이성의 사도로 성장하고 있었습니다.

◼︎   나의 첫 수학적 사고 ◼︎

2016년 한국.

14세의 소년이 책상에 앉아 가만히 생각하고 있습니다. 늘 그랬듯이 수학과 물리에 관한 잡생각에 빠져 있었지요. 이날은 소년의 생각이 매우 뜻밖의 지점까지 도달했습니다.

지금까지 선명하게 기억나는 순간이에요. 저의 첫 수학적, 철학적 사유가 일어났던 순간이라고 할 수 있겠어요. 이날 생각이 여기까지 닿자 저는 소스라치게 놀랐습니다. 만약 이 생각이 맞다면 우리의 세계관을 이루는 수많은 개념을 폐기해야만 하니까요. 선과 악의 문제, 처벌과 보상의 정당성, 삶의 의미마저 모두 불분명해집니다.

그러나 저는 이 생각 앞에서 무기력감보다는 경탄과 호기심을 더 크게 느꼈습니다. 이 생각은 몇 가지 가정에 의존합니다. 모든 물리 법칙은 수식으로 표현할 수 있다는 가정이 필요하고, 물리 법칙의 지배를 받지 않은 개체는 없다는 가정도 필요합니다. 과연 이 가정들이 참이라고 확신할 수 있을까요?

돌이켜 보면 이런 의문에 답을 찾고 싶다는 마음이 제가 학창 시절 수학, 물리학 그리고 철학을 열심히 공부한 동기였다는 생각이 듭니다. 제가 KAIST에 입학하고 교환학생 신분으로 영국으로 가도록 이끌어준 원동력이었던 것이죠. 종교를 향한 회의로 출발한 러셀의 성찰이 그가 세계적인 수리철학자로 발돋움하는 밑거름을 마련해 주었듯이 말이에요.

◼︎ 지식을 향한 열망 ◼︎

그리스어 연습장을 한창 작성하던 16세에 러셀은 입대를 준비하는 학생들이 다니는 육군 예비학교에 입학합니다. 안정적인 공간에서 영국 케임브리지대학교 수학과 입학시험을 준비하기 위해서였죠. 그러나 이곳의 생활은 러셀에게 전혀 맞지 않았습니다. 대부분의 예비학교 학생들은 공부에 관심이 없는 나이 많은 형들이었고, 그들은 나이가 어린 데다가 범생이 같은 러셀을 수시로 놀렸습니다. 가정에서는 종교적으로, 학교에서는 사회적으로 고립된 러셀은 극심한 외로움과 우울감을 느꼈습니다.

학교에는 고원으로 가는 작은 길이 있었습니다. 수업이 끝나고 해질녘이 되면 러셀은 혼자서 그 길을 올라가고는 언덕에 앉아 저무는 해를 보며 극단적인 선택마저 고민했습니다. 하지만 러셀은 그런 선택은 하지 않았어요. 러셀은 수학을 더 알고 싶었기 때문이라고 말했습니다. 이렇게나 지식을 향한 열망이 강했던 소년은, 1890년 10월 케임브리지대학교에 합격합니다.

※글쓴이 소개

최정담. 수학 베스트셀러 <;발칙한 수학책>;의 저자 최정담은 수학 대중화에 관심이 많은 KAIST 수리과학과 학생입니다. 영국의 수학자이자 철학자인 버트런드 러셀을 좋아해 이번 연재를 통해 러셀의 생애를 소개합니다.