d라이브러리

여러분 혹시 ‘마방진’을 알고 계신가요? 마방진은 우리가 즐겨 푸는 스도쿠와 비슷합니다. 가로세로 n칸씩 총 n²칸으로 이뤄진 표에 1부터 n²까지의  자연수를 배열하는 숫자 퍼즐이죠. 단, 배열했을 때 각 행과 열 그리고 대각선에 적힌 수의 ‘합’이 모두 같아야 합니다.

저라면 수의 배열을 일일이 바꿔가며 마방진을 찾을 것 같은데요. n이 커지면 이런 방법으로 마방진을 찾는 건 어렵다고 합니다. n이 9만 돼도 총 81!(=81×80×…×2×1)개 배열을 따져야 하는데, 슈퍼컴퓨터도 벅찰 정도로 계산량이 많거든요. 다른 방법을 찾아봐야겠죠?

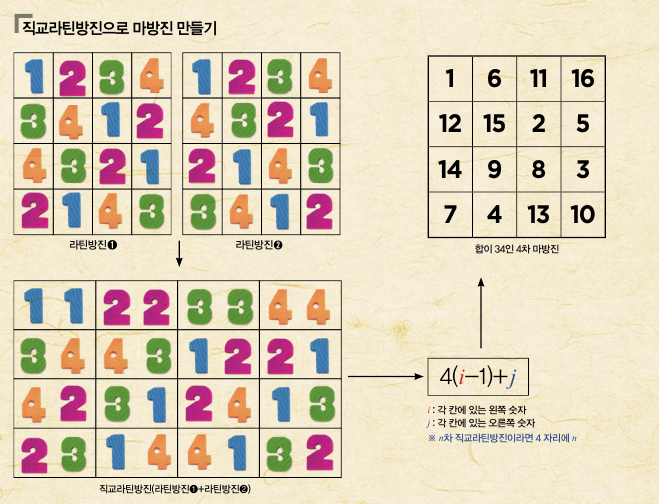
마방진을 찾는 방법 중 하나는 마방진보다 간단한 수의 배열인 ‘직교라틴방진’을 먼저 찾는 겁니다. 어떤 경우 직교라틴방진에서 간단한 계산만 하면 마방진을 만들 수 있거든요. 라틴방진은 칸이 n²개인 표에 1부터 n까지의 자연수를 각 행과 열에 같은 숫자가 들어가지 않게 배열한 거예요.

직교라틴방진은 칸 수가 같은 라틴방진 2개를 하나로 합한 겁니다. 2개의 라틴방진에서 같은 위치에 있는 두 숫자를 순서쌍처럼 한 칸에 차례대로 넣는 거지요. 이렇게 전부 순서쌍으로 나타냈을 때 겹치는 순서쌍이 하나도 없어야 해요. 

얼마 전까지만 해도 스위스 수학자 레온하르트 오일러의 직교라틴방진이 가장 오래됐다고 알려져 있었습니다. 하지만 2006년 여러 수학자와 과학자가 노력한 끝에 오일러보다 무려 61년 앞서 최석정이 가로세로가 9칸인 ‘9차 직교라틴방진’을 만들었다는 것을 전 세계에 알렸습니다.

누가 먼저 알고 있었는지 따질 만큼 직교라틴방진이 중요한 이유는 ‘조합론 디자인’의 효시로 보기 때문인데요. 조합론 디자인은 반도체칩 설계부터 이동통신 시스템 구축까지 다양한 분야에 활용되는 수학의 한 분야라고 합니다. 

최근 김종락 교수님께서 최석정의 직교라틴방진에 관한 새로운 연구를 하셨다면서요?