
매직 티켓을 들고 2D 어드벤처로 갔어. 이곳을 제대로 즐기려면 변신이 필요하다며, 열매 하나를 줬어. 그런데 열매를 꿀컥 삼킨 순간, 우리 몸이 좁쌀만 하게 작아졌지 뭐야. 마치 허허 벌판에 놓인 점 하나처럼 키는 0cm고 바닥에 딱 붙어 걸어 다니는 사람이 된 거야. 달리기는 물론 뛰는 것도 불가능해. 으악~! 원래대로 돌아올 수 있는 거지? 그래도 앤트맨 의상은 마음에 들어.
교생쌤의 설명에 따르면 2차원 면으로 이뤄진 클라인 병 표면을 탐험하려면 우리가 점이어야 해서 그렇대. 키를 잴 수 있는 사람은 위, 아래라는 방향이 있기 때문에 클라인 병 위를 제대로 돌아다닐 수 없다는 거야.
뫼비우스 띠 위를 기어 다니는 개미 그림을 본 적 있지? 수학을 소재로 작품 활동을 해서 유명한 네덜란드의 판화가 마우리츠 에스허르의 대표작 중 하나인데, 여기서 개미를 그린 것도 우리가 개미처럼 작아진 것과 같은 이유에서래. 여태껏 작가가 개미를 좋아해서 그린 줄 알았어. 수학적 의미가 있었다니 놀랍지?
영상이 상영되기 시작했어. 아까 우리가 탔던 롤러코스터 모습이야. 깩깩 소리를 지르느라 몰랐는데, 무서워하는 모습을 영상으로 담았더라고. 친구들의 모습은 웃겼지만, 내 얼굴이 나올 땐 부끄러워 어찌해야 할지 모르겠더라. 그런데 갑자기 클라인 병의 모습이 사각형으로 바뀌었어. 사각형에 화살표 표시만 있는데 이게 클라인 병이래. 대체 어떻게 된 거지?
위상수학자 따라서 클라인 병 그리자!
배배 꼬인 클라인 병을 제대로 그리기란 매우 어려워요. 그런데 위상수학자는 클라인 병의 성질을 모두 나타내면서도 아주 쉽게 그림을 그린답니다. 그 비결은 클라인 병이 2차원 다양체라는 데 있어요. 면으로 이뤄진 만큼 사각형 하나로도 모든 걸 나타낼 수 있거든요. 바로 클라인 병으로 가면 어려우니 원기둥부터 하나하나 살펴볼게요.
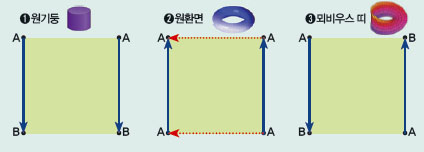
➊사각형의 꼭짓점에 같은 알파벳이 쓰여 있다면 둘은 한 점이에요.
즉 서로 연결됐다는 뜻이죠. 따라서 사각형을 같은 점끼리 붙이는데, 화살표가 같은 방향으로 겹치도록 말면 원기둥이 만들어져요.
➋이번엔 모든 점이 같아요. 먼저 원기둥을 만들고, 화살표가 같은 방향으로 겹치게 원기둥을 말면 원환면이 완성된답니다.
➌뫼비우스 띠는 원기둥에서 화살표 방향만 달라요. 화살표 방향이 같게 사각형을 비틀면 뫼비우스 띠가 되겠죠?
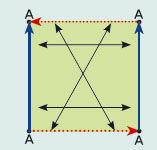
이제 사각형으로 클라인 병을 만들 준비는 다 됐어요. 사각형 중에 어떤 꼭짓점이 같아야 할까요? 화살표는 어떻게 그려야 할까요?
정답은 원환면에서 화살표 방향 하나만 바꾸면 된답니다. 그래서 클라인 병을 원환면을 비튼 거라고 말하지요. 이제 이 위를 걸어 볼게요.
가로로는 언제나 똑바로 걷게 돼 있어요. 그런데 왼쪽 변과 만나면 오른쪽 변으로 나오고 오른쪽 변과 만나면 왼쪽 변으로 나와요. 세로로는 항상 대각선으로 걷게 돼요. 윗변으로 들어가면 마주보는 대각선 아랫변으로 나온답니다.
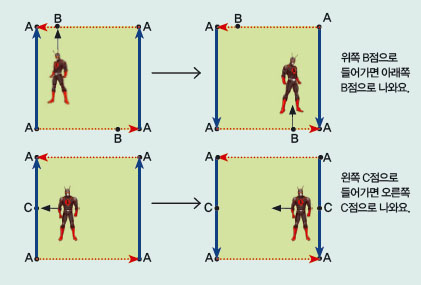
클라인 병 위를 한 바퀴 돌고 나면 개미인간은 주변과 비교해 좌우가 바뀌어요.
▼


클라인 병 = 뫼비우스 띠 + 뫼비우스 띠
클라인 병 위를 걷고 있는데, 누군가 클라인 병을 가위질하기 시작했어. 싹둑싹둑 종이 자르는 소리가 천둥소리보다 크게 들려~! 거대 가위를 피해 도망 다니느라 몰랐는데, 누군가 클라인 병을 삼등분했나봐. 난 가운데, 교생쌤은 위쪽에, 절친은 아래쪽에 있었는데, 모두 다 떨어졌거든.
일단 나는 하염없이 걷기 시작했어. 위아래로 가면 막다른 길에 들어서고, 옆으로 가면 대각선으로 걷게 되네. 아무래도 여긴 뫼비우스 띠인가 봐. 이상하네. 분명 클라인 병을 반으로 잘랐을 때 뫼비우스 띠가 된다고 했는데…. 어째서 삼등분 했는데도 뫼비우스 띠가 되지?
교생쌤과 절친이 있는 곳도 뫼비우스 띠 위인지 물어봤어. 그런데 거긴 아니래. 교생쌤이 있었던 위쪽은 끝없이 길이 이어져있대. 아무리 걸어도 길이 있다는 거야. 신기한 건 절친이 있는 곳은 아래쪽이 그렇대. 둘 다 옆으로 가면 대각선으로 걷게 된대. 교생쌤 말로는 본인이 있는 곳과 절친이 있는 곳을 연결해야 뫼비우스 띠래.
▼관련기사를 계속 보시려면?











