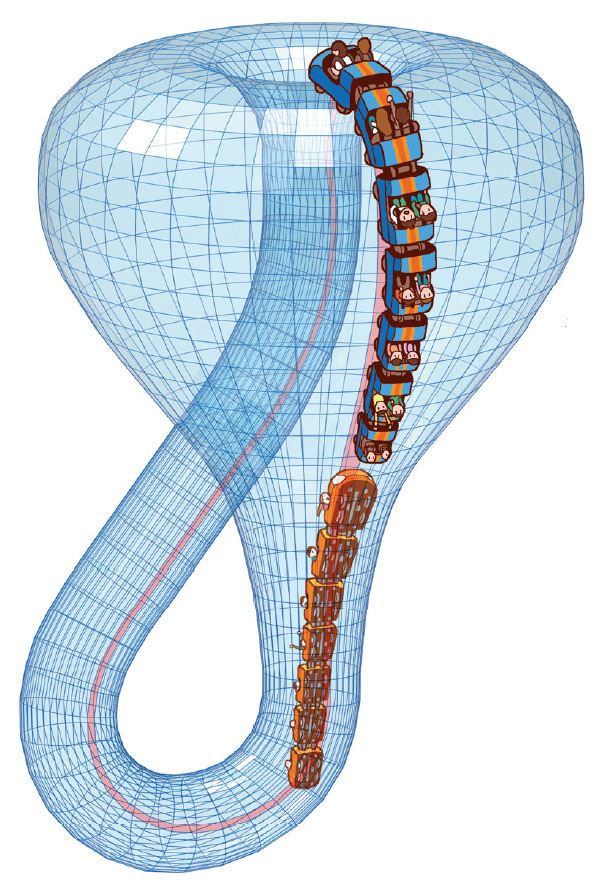
보통 롤러코스터는 꼬불꼬불 꼬인 레일이 눈에 띄잖아. 그런데 클라인 병 롤러코스터는 클라인 병 내부를 여행해서 그런지 레일보다는 구조물이 시선을 강탈했어. 어찌나 큰지 내가 개미 같았다니까. 엘리베이터를 타고 꼭대기에 올라가 롤러코스터를 탔어. 으, 아찔해. 블랙홀을 연상케 같은 구멍 아래로 롤러코스터가 내려가나 봐.
드드드… 슝~, 예상이 맞았어. 시작부터 절벽 아래로 떨어져~. 끝없이 펼치지는 좁은 터널을 거의 90°로 내려오니까 심장이 내려앉는 기분이었어. 밀실 공포까지 더해져 몸에 있는 털이란 털은 모두 곤두섰지 뭐야. 대체 이 터널의 끝은 어디인 거야? 이제 다시 위로 올라가네.
그런데 말이야, 분명 한 바퀴를 돌아 출발점으로 돌아온 거 같은데 내가 안쪽에 있어. 레일의 반댓면에 붙어서 달리고 있어. 어떻게 된 걸까?
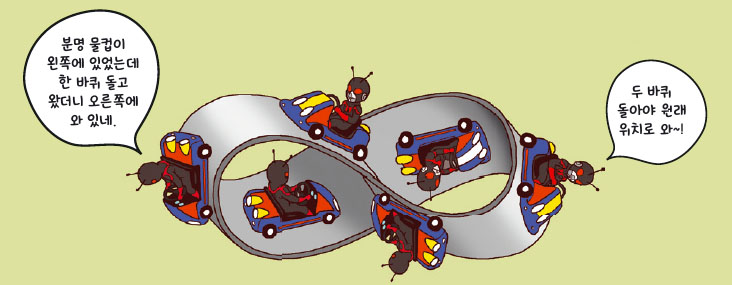
친구들 모두 신기한 경험을 한 탓인지 수학 교생쌤에게 질문이 쏟아졌어. 쌤은 ‘뫼비우스 띠’를 떠올리면 그 원리를 이해하기 쉽다고 이야기해줬지. 뫼비우스 띠로 만들어진 도로를 상상해봐. 쭉 뻗은 길인가 싶더니 언덕길과 내리막길이 반복해서 나와. 도로 위를 차로 달리다보면 180°로 몸이 비틀어지는 것도 같고, 거꾸로 서는 느낌이 들어.
또 분명 한 바퀴 돌았는데 정확히 나는 출발지의 도로면 반대편에 있어. 이처럼 한 바퀴를 돌아왔을 때 안과 밖이 바뀌는 성질을 ‘비가향’이라고 한대. 즉 클라인 병 롤러코스터도 비가향인거야.

뫼비우스 띠가 있으면 같은 종족
클라인 병은 면으로 둘러싸인 곡면으로, 4차원에 살아요. 1882년 독일 수학자 펠릭스 클라인이 발견했어요. 뫼비우스 띠가 원통형 띠를 꼰 거라면 클라인 병은 도넛 모양의 원환면을 비튼 거예요.
그런데 위상수학자는 3차원의 뫼비우스 띠와 4차원의 클라인 병을 모두 ‘2차원 다양체’라고 불러요. 어느 지점에서 주변을 봐도 면으로 이뤄졌기 때문이에요. 도형의 일부를 봤을 때 선, 면, 공간처럼 유클리드 공간이 보이면 그 도형을 ‘다양체’라고 하는데, 보이는 유클리드 공간이 선이면 1차원 다양체, 면이면 2차원 다양체, 3차원 공간이면 3차원 다양체라고 하거든요. 그래서 속이 빈 원환면(도넛 모양의 도형)과 구, 원기둥도 2차원 다양체랍니다.
위상수학자가 이런 다양체를 맞닥뜨렸을 때 가장 먼저 하는 일은 가향인지, 비가향인지 따지는 거예요. 가향이냐 비가향이냐에 따라쓰는 수학 정리가 다른 경우가 많기 때문이에요. 따라서 출발지부터 한 바퀴를 돌았을 때 같은 방향으로 돌아올 수 있는지 살펴요. 항상 같은 방향으로 돌아올 수 있으면 가향, 반대 방향으로 돌아올 수 있으면 비가향이에요. 가향의 대표적인 2차원 다양체가 구나 원기둥, 원환면이랍니다.
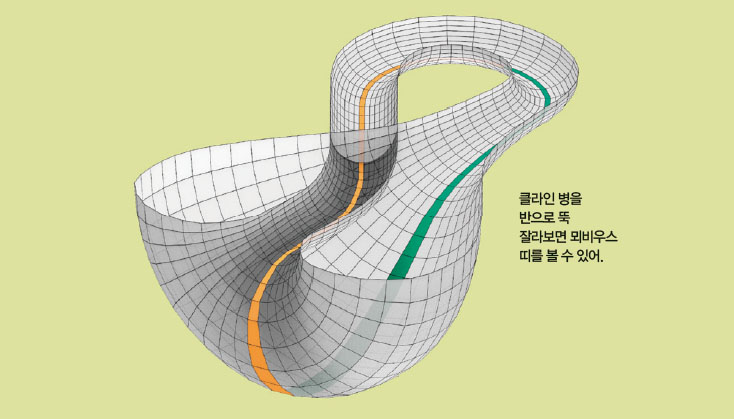
앞에서 소개한 대로 뫼비우스 띠와 클라인 병은 비가향 다양체예요. 아까 클라인 병을 이해하는 데 뫼비우스 띠가 좋은 예라고 했죠. 그 이유는 2차원 다양체가 뫼비우스 띠를 품고 있으면 비가향 다양체기 때문이에 롤러코스터요. 클라인 병을 반으로 딱 잘라서 보면 양쪽으로 늘어난 뫼비우스 띠를 볼 수 있답니다.
▼관련기사를 계속 보시려면?