2D 어드벤처를 나서자 몸은 원래대로 돌아왔어. 당연히 그럴 거라고 예상했지만 혹시나 하는 마음에 불안했던 것도 사실이야. 어쨌든 열심히 놀았더니 배꼽시계가 요란하게 소리를 내지 뭐야. 튤립 정원에서 도시락을 먹기로 했어.
빨간꽃, 분홍꽃, 보라꽃. 형형색색의 튤립이 우리 눈을 사로잡았어. 꽃향기에 취해 밥을 먹고 있는데 교생쌤이 재밌는 이야기를 해주셨어. 그 유명한 ‘4색 정리’가 클라인 병 위에서는 안 통한다는 거야. 이상하지 않아? 정리면 어떤 상황에서도 통해야 하는데 안 되는 게 있다니!
알고 보니 내가 4색 정리에 대해 내가 제대로 복습도 중요하니까 말이야. 몰랐더라고. 너흰 4색 정리에 대해 어떻게 알고 있니?
난 어떤 지도든 서로 맞닿은 구역이 서로 다른 색이 되도록 만드는 데 4색이면 충분하다는 걸로 고 있어서, 클라인 병에 그린 지도도 당연히 4색이면 되는 줄 알았어. 근데 본래 문제가 평면에 그린 지도만 가능하다는 거였대. 클라인 병은 곡면이잖아. 애초에 4색 정리와 관련이 없었던 거지.
오히려 클라인 병은 곡면 위에 그린 지도에 관한 ‘히우드 추측’을 깨부쉈대. 영국 수학자 퍼시 히우드는 오일러 지표 χ(꼭짓점의 수-변의 수+면의 수)가 양수가 아닌 곡면, 즉 구면을 제외한 모든 곡면 위에 그린 지도는
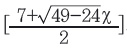
가지 색이면 충분히 칠할 수 있고, 이보다 적은 색으로는 색칠할 수 없는 지도가 있다고 추측했어. 여기서 [x]는 실수 x를 넘지 않는 최대 정수를 말해. 예를 들어 [2.5]=2, [-2.5]=-3이지.
히우드 추측의 유일한 예외
그런데 미국 수학자 필립스 프랭클린이 클라인 병에 그린 어떤 지도도 6색이면 충분하다는 걸 증명한 거야. 클라인 병은 서로 다른 꼭짓점이 1개, 변이 2개, 면이 1개니까 오일러 지표가 1-2+1=0이야. 히우드 공식의 χ자리에 0을 대입하면
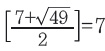
이 나와. 근데 이보다 한 색이 적은 6색으로도 클라인 병 위에 그린 어떤 지도도 색칠할 수 있는거지.
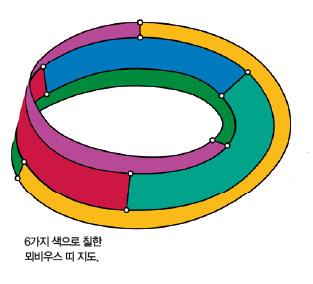
프랭클린은 이 같은 사실을 밝히면서 클라인 병 위에서 5색으로 칠할 수 없는 지도도 제시했어. 그게 바로 아래 지도야. 1과 3, 4와 6이 이웃한 구역이라는 걸 염두하고 살펴보렴. 또 점 C는 구역 3과 4, 6에, 점 D는 1과 4, 6에 모두 걸친다는 걸 유념하면 이해가 될 거야.
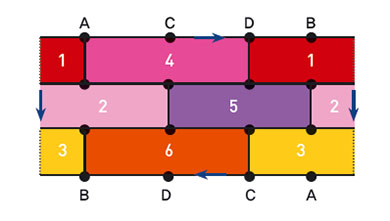
이후 독일 수학자 게르하르트 링겔과 미국 수학자 존테오도르 영스가 클라인 병을 제외하면 히우드 추측이 모든 경우에 성립한다는 걸 증명했어.
그러고 보니 여기 튤립 정원 말이야. 프랭클린이 찾은 지도대로 구역을 나눠서 서로 다른 색의 튤립을 심어 놓았어. 그래서 교생쌤이 4색 정리 이야기를 꺼냈나봐. 사실 클라인 병에 관한 연구는 아직도 활발히 진행되고 있대. 2017년에는 n차원 클라인 병이 어떤 차원에서 매장되고 몰입될 수 있는지 설명한 연구가 나왔어. 먼 훗날 이 놀이공원을 다시 찾으면 더 재밌는 놀이기구로 가득할지도 몰라.
배가 부르니 잠이 온다. 왠지 꿈에서 2차원이나 4차원을 여행할 것만 같아. 따뜻한 햇볕을 맞으며 한 숨 자고 일어나서 클라인 병 롤러코스터를 한번 더 타야겠어. 복습도 중요하니까 말이야.
▼관련기사를 계속 보시려면?











