
로댕의 ‘생각하는 사람’, ‘밀로의 비너스’처럼 아름다운 조각품도 조각가의 손이 닿기 전에는 볼품없는 청동이나 석고 덩어리였다. 보석도 마찬가지다. 누군가의 손이 닿기 전에는 그저 그런 돌멩이였다. 과연 돌멩이를 아름다운 보석으로 만들어준 조각가는 누구일까? 이 솜씨 좋은 조각가의 정체는 바로 수학이다.
 아름다운 보석을 조각하려면 먼저 알맞은 재료부터 골라야 합니다. 조각가들은 모래, 과일, 심지어 연필심으로도 작품을 만들지만 보석은 조금 다릅니다. 어떤 재료가 보석이 될 수 있을까요?
아름다운 보석을 조각하려면 먼저 알맞은 재료부터 골라야 합니다. 조각가들은 모래, 과일, 심지어 연필심으로도 작품을 만들지만 보석은 조금 다릅니다. 어떤 재료가 보석이 될 수 있을까요?
광물과 결정. 비슷해 보이지만 미묘하게 다른 두 단어에 비밀이 숨어있습니다. 우리 주위에 있는 고체는 물질을 구성하는 원소들이 육면체나 육각기둥 모양으로 규칙적으로 배열된 ‘결정질’과 특정한 모양 없이 제멋대로 나열된 ‘비정질’로 나뉩니다. 결정질 고체 중 자연에서 저절로 만들어지는 물질이 바로 광물입니다. 이 중 우리 눈을 한 번에 사로잡을 정도로 아름다운 광물만 보석이 될 수 있죠.
대칭으로 줄 세우기
지금까지 발견된 광물은 무려 4000여 종이나 됩니다. 보석을 조각하기에 앞서 이 수많은 광물을 분류하는 게 먼저입니다. 광물의 종류만큼 결정의 모양도 다양해서 모양보다는 결정이 가지는 ‘대칭성’을 기준으로 분류합니다.
결정에서 말하는 대칭은 우리가 알고 있는 대칭과 조금 다릅니다. 점이나 선을 기준으로 양쪽 모양이 똑같은 대칭이 아니라, 점이나 선을 기준으로 회전했을 때 처음 모양과 겹치는 대칭을 말합니다. 예를 들어 정삼각형은 무게 중심을 기준으로 120°, 360°회전하면 원래 모양과 겹치므로 대칭성이 있다고 합니다. 결정 모양에 따라 대칭의 기준이 다르고 360° 회전했을 때 처음 모양과 일치하는 횟수도 다릅니다.
대칭의 기준이 되는 결정축★의 길이, 각도에 따라 광물을 6가지로 분류합니다. 이 방법은 독일의 광물학자 크리스티안 바이스가 고안한 것으로 광물을 총 6가지로 분류하기 때문에 ‘6정계’라고 합니다. 결정의 모양을 연구한 수학자도 있습니다. 19세기 폴란드 수학자 아서 쇤플리스와 러시아 수학자 에그래프 표도로프는 대수학의 ‘군’ 개념을 이용해 광물을 분류했습니다. 점, 선을 기준으로 모든 대칭을 고려하면 광물을 총 230개로 분류할 수 있다고 밝혔지요.
결정축★ 결정의 중심을 통과하는 가상의 선. 이 선을 기준으로 결정을 360° 회전시켰을 때 처음 모양과 2번 이상 겹쳐야 한다.
 아름다운 보석을 조각하려면 먼저 알맞은 재료부터 골라야 합니다. 조각가들은 모래, 과일, 심지어 연필심으로도 작품을 만들지만 보석은 조금 다릅니다. 어떤 재료가 보석이 될 수 있을까요?
아름다운 보석을 조각하려면 먼저 알맞은 재료부터 골라야 합니다. 조각가들은 모래, 과일, 심지어 연필심으로도 작품을 만들지만 보석은 조금 다릅니다. 어떤 재료가 보석이 될 수 있을까요?광물과 결정. 비슷해 보이지만 미묘하게 다른 두 단어에 비밀이 숨어있습니다. 우리 주위에 있는 고체는 물질을 구성하는 원소들이 육면체나 육각기둥 모양으로 규칙적으로 배열된 ‘결정질’과 특정한 모양 없이 제멋대로 나열된 ‘비정질’로 나뉩니다. 결정질 고체 중 자연에서 저절로 만들어지는 물질이 바로 광물입니다. 이 중 우리 눈을 한 번에 사로잡을 정도로 아름다운 광물만 보석이 될 수 있죠.
대칭으로 줄 세우기
지금까지 발견된 광물은 무려 4000여 종이나 됩니다. 보석을 조각하기에 앞서 이 수많은 광물을 분류하는 게 먼저입니다. 광물의 종류만큼 결정의 모양도 다양해서 모양보다는 결정이 가지는 ‘대칭성’을 기준으로 분류합니다.
결정에서 말하는 대칭은 우리가 알고 있는 대칭과 조금 다릅니다. 점이나 선을 기준으로 양쪽 모양이 똑같은 대칭이 아니라, 점이나 선을 기준으로 회전했을 때 처음 모양과 겹치는 대칭을 말합니다. 예를 들어 정삼각형은 무게 중심을 기준으로 120°, 360°회전하면 원래 모양과 겹치므로 대칭성이 있다고 합니다. 결정 모양에 따라 대칭의 기준이 다르고 360° 회전했을 때 처음 모양과 일치하는 횟수도 다릅니다.
대칭의 기준이 되는 결정축★의 길이, 각도에 따라 광물을 6가지로 분류합니다. 이 방법은 독일의 광물학자 크리스티안 바이스가 고안한 것으로 광물을 총 6가지로 분류하기 때문에 ‘6정계’라고 합니다. 결정의 모양을 연구한 수학자도 있습니다. 19세기 폴란드 수학자 아서 쇤플리스와 러시아 수학자 에그래프 표도로프는 대수학의 ‘군’ 개념을 이용해 광물을 분류했습니다. 점, 선을 기준으로 모든 대칭을 고려하면 광물을 총 230개로 분류할 수 있다고 밝혔지요.
결정축★ 결정의 중심을 통과하는 가상의 선. 이 선을 기준으로 결정을 360° 회전시켰을 때 처음 모양과 2번 이상 겹쳐야 한다.

쌩얼이 빛나는 비결
TV 프로그램을 보면 종종 ‘원석을 발견했다’, ‘예능 원석을 찾았다’고 합니다. 아직 능숙하지 않지만 재능이 뛰어난 신인이나 아마추어를 ‘원석’이라고 표현하죠. 원석은 보석과 밀접하게 관련 있는 말입니다. 수많은 광물 중 아직 보석이 아니지만, 잘 가공하면 보석으로 태어날 수 있는 광물이 바로 원석이지요. 원석을 찾았으면 이제 아름다운 보석으로 만들어야 합니다.
 맨 얼굴에 화장하면 예뻐지지만 보석은 오히려 원석을 깎아 맨 얼굴을 드러내야 아름답습니다. 흔히 말하는 ‘쌩얼 미인’이 바로 보석인 셈입니다. 그런데 보석은 원석이 가진 특징에 맞게 조각해야 합니다. 얼굴이 가진 특징이 얼굴형, 이목구비, 피부색이라면 원석이 가진 특징은 바로 ‘각도’입니다.
맨 얼굴에 화장하면 예뻐지지만 보석은 오히려 원석을 깎아 맨 얼굴을 드러내야 아름답습니다. 흔히 말하는 ‘쌩얼 미인’이 바로 보석인 셈입니다. 그런데 보석은 원석이 가진 특징에 맞게 조각해야 합니다. 얼굴이 가진 특징이 얼굴형, 이목구비, 피부색이라면 원석이 가진 특징은 바로 ‘각도’입니다.
TV 프로그램을 보면 종종 ‘원석을 발견했다’, ‘예능 원석을 찾았다’고 합니다. 아직 능숙하지 않지만 재능이 뛰어난 신인이나 아마추어를 ‘원석’이라고 표현하죠. 원석은 보석과 밀접하게 관련 있는 말입니다. 수많은 광물 중 아직 보석이 아니지만, 잘 가공하면 보석으로 태어날 수 있는 광물이 바로 원석이지요. 원석을 찾았으면 이제 아름다운 보석으로 만들어야 합니다.
 맨 얼굴에 화장하면 예뻐지지만 보석은 오히려 원석을 깎아 맨 얼굴을 드러내야 아름답습니다. 흔히 말하는 ‘쌩얼 미인’이 바로 보석인 셈입니다. 그런데 보석은 원석이 가진 특징에 맞게 조각해야 합니다. 얼굴이 가진 특징이 얼굴형, 이목구비, 피부색이라면 원석이 가진 특징은 바로 ‘각도’입니다.
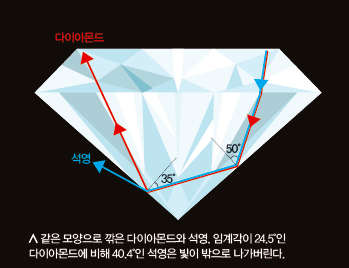
맨 얼굴에 화장하면 예뻐지지만 보석은 오히려 원석을 깎아 맨 얼굴을 드러내야 아름답습니다. 흔히 말하는 ‘쌩얼 미인’이 바로 보석인 셈입니다. 그런데 보석은 원석이 가진 특징에 맞게 조각해야 합니다. 얼굴이 가진 특징이 얼굴형, 이목구비, 피부색이라면 원석이 가진 특징은 바로 ‘각도’입니다.각도는 보석의 광채를 결정하는 중요한 요소입니다. 빛은 보석 안으로 들어가거나 보석 밖으로 나갈 때 굴절돼 방향이 꺾입니다. 그런데 어떤 보석이냐에 따라 빛이 꺾이는 각도가 다릅니다. 가끔 보석 내부로 들어온 빛이 보석의 면에 수직인 선과 이루는 각도가 일정 값보다 크면 밖으로 나가지 못하고 다시 내부로 튕겨 들어오는데, 이 각도의 크기를 ‘임계각’이라고 합니다. 보석을 조각할 때 임계각에 맞춰 조각하면 빛이 보석 안에 머무르기 때문에 더욱 반짝반짝 빛나게 됩니다.
보석 깎는 조각가, 수학
임계각을 계산해 광채를 높인 세공 방법이 ‘브릴리언트 커트’입니다. 브릴리언트 커트는 주로 다이아몬드를 깎을 때 사용하는 방법으로, 윗부분은 마치 왕관처럼 둥글고 아래는 뾰족합니다. 이 모양은 1700년 이탈리아의 다이아몬드 연마사 빈센트 페루치가 고안했습니다. 이후 여러 학자가 광채를 최대로 할 수 있는 비율과 면의 개수를 수학적으로 계산해 58개의 평평한 면으로 이뤄진 현재 모양을 갖게 됐습니다.
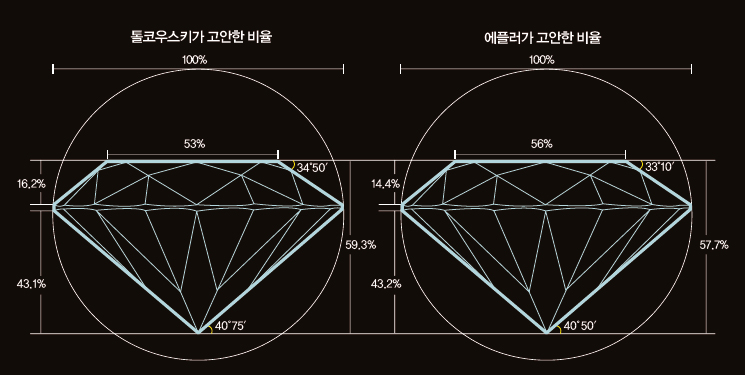
다만 나라마다 아름다움의 기준이 다르므로 각도와 비율에 차이가 있습니다. 미국에서는 1919년 벨기에의 공학자이자 수학자인 마르셀 톨코우스키가 고안한 비율을, 유럽에서는 1939년 독일의 광물학자 빌헬름 에플러가 고안한 비율로 다이아몬드를 조각합니다.
보석 깎는 조각가, 수학
임계각을 계산해 광채를 높인 세공 방법이 ‘브릴리언트 커트’입니다. 브릴리언트 커트는 주로 다이아몬드를 깎을 때 사용하는 방법으로, 윗부분은 마치 왕관처럼 둥글고 아래는 뾰족합니다. 이 모양은 1700년 이탈리아의 다이아몬드 연마사 빈센트 페루치가 고안했습니다. 이후 여러 학자가 광채를 최대로 할 수 있는 비율과 면의 개수를 수학적으로 계산해 58개의 평평한 면으로 이뤄진 현재 모양을 갖게 됐습니다.
다만 나라마다 아름다움의 기준이 다르므로 각도와 비율에 차이가 있습니다. 미국에서는 1919년 벨기에의 공학자이자 수학자인 마르셀 톨코우스키가 고안한 비율을, 유럽에서는 1939년 독일의 광물학자 빌헬름 에플러가 고안한 비율로 다이아몬드를 조각합니다.
 그런데 모든 다이아몬드가 브릴리언트 커트 모양인 것은 아닙니다. 네모난 모양이 있는 반면 하트 모양의 다이아몬드도 있죠. 게다가 사파이어, 루비 같은 보석은 광채를 최대로 할 수 있는 고유의 모양 없이 직사각형이나 원 또는 타원 모양이 대부분입니다. 이유가 무엇일까요?
그런데 모든 다이아몬드가 브릴리언트 커트 모양인 것은 아닙니다. 네모난 모양이 있는 반면 하트 모양의 다이아몬드도 있죠. 게다가 사파이어, 루비 같은 보석은 광채를 최대로 할 수 있는 고유의 모양 없이 직사각형이나 원 또는 타원 모양이 대부분입니다. 이유가 무엇일까요?
보석 세공사는 미리 계산한 비율과 각도에 맞춰 보석을 조각한다.
광채가 먼저냐, 무게가 먼저냐
보석의 값어치를 결정하는 요소 중 광채만큼 중요한 것이 중량입니다. 수많은 광물 중 보석이 될 수 있는 건 단 몇백 개뿐인데, 이마저도 쉽게 얻을 수 없습니다. 우리나라만 해도 연옥, 자수정, 사문석 정도가 발굴될 뿐 다이아몬드나 사파이어의 원석은 거의 찾을 수 없으니까요. 다이아몬드의 대표 산지인 남아프리카와 캐나다도 손톱보다 작은 다이아몬드 원석을 얻기 위해 많은 노력을 해야 합니다. 모든 다이아몬드를 브릴리언트 커트로 깎을 수 없는 이유가 여기에 있습니다.
보석의 가치를 높이려면 원석에서 최대한 큰 보석을 얻어내야 합니다. 그런데 우리가 얻어내는 원석은 모양이 제각각이라서 브릴리언트 커트를 고집하면 곤란합니다. 길쭉한 원석을 둥근 모양으로 깎으면 나머지는 버려야 하니까요. 광채가 덜하더라도 중량이 크면 더 비싼 값을 받을 수 있으므로 힘들게 얻은 원석을 낭비하지 않기 위해 최대한 많은 중량을 얻을 수 있도록 조각해야 합니다. 특히 사파이어나 루비처럼 색이 중요한 보석들은 광채보다 중량을 우선해, 대부분 원석의 모양에 맞춰 타원이나 사각형으로 조각합니다.
쿠키를 만들어 본 적 있나요? 넓게 편 밀가루 반죽 위에 모양틀을 도장처럼 찍으면 별, 하트 모양의 반죽이 뚝뚝 떨어져 나옵니다. 그런데 틀을 무턱대고 찍으면 안 됩니다. 반죽의 크기는 정해져 있어서 틀을 최대한 바짝 붙여 찍어야 많은 쿠키를 만들 수 있습니다. 원석에서 중량이 큰 보석을 만드는 일도 반죽을 찍는 일과 비슷합니다. 보석을 원, 타원, 브릴리언트 커트 등 어떤 모양으로 조각할지 결정했으면 원석에서 가장 큰 보석이 나오도록 위치와 방향을 잘 맞춰야 합니다.

보석계 알뜰 살림꾼, 최적화 이론
이렇게 정해진 조건 안에서 최댓값 또는 최솟값을 구하는 문제를 수학에서는 ‘최적화 문제’라고 합니다. 주어진 구간에서 함수의 최댓값과 최솟 값을 구하는 문제도 일종의 최적화 문제라고 할 수 있지요.
최적화 문제 중 조건이 무수히 많은 경우를 ‘반무한 최적화 문제’라고 하는데, 원석에서 가장 큰 보석을 조각하는 문제가 여기에 속합니다. 제멋대로 생긴 원석을 조각할 수 있는 방향이 무한개이기 때문이지요.
반무한 최적화 문제는 조건이 많기 때문에 일반적인 최적화 문제보다 풀기 어렵습니다. 학자들은 컴퓨터 알고리즘을 이용해 반무한 최적화 문제의 근사해를 찾았는데, 이 방법을 이용해 조각하자 이전에 얻었던 중량보다 더 무거운 보석을 얻을 수 있게 됐습니다. 수학 덕분에 어렵게 얻은 원석을 최대한 낭비하지 않게 된 겁니다.
보석을 조각하는 수학의 뛰어난 솜씨, 잘 감상 하셨나요? 이렇게 아름다운 보석이 만들어지는 모든 과정에는 수학의 손길이 필요합니다. 가끔은 보석의 아름다운 외모뿐 아니라 내면을 들여다보는 여유를 가져 보세요. 아름다운 보석 뒤에는 똑똑한 조각가 수학이 숨어있습니다.
보석의 값어치를 결정하는 요소 중 광채만큼 중요한 것이 중량입니다. 수많은 광물 중 보석이 될 수 있는 건 단 몇백 개뿐인데, 이마저도 쉽게 얻을 수 없습니다. 우리나라만 해도 연옥, 자수정, 사문석 정도가 발굴될 뿐 다이아몬드나 사파이어의 원석은 거의 찾을 수 없으니까요. 다이아몬드의 대표 산지인 남아프리카와 캐나다도 손톱보다 작은 다이아몬드 원석을 얻기 위해 많은 노력을 해야 합니다. 모든 다이아몬드를 브릴리언트 커트로 깎을 수 없는 이유가 여기에 있습니다.
보석의 가치를 높이려면 원석에서 최대한 큰 보석을 얻어내야 합니다. 그런데 우리가 얻어내는 원석은 모양이 제각각이라서 브릴리언트 커트를 고집하면 곤란합니다. 길쭉한 원석을 둥근 모양으로 깎으면 나머지는 버려야 하니까요. 광채가 덜하더라도 중량이 크면 더 비싼 값을 받을 수 있으므로 힘들게 얻은 원석을 낭비하지 않기 위해 최대한 많은 중량을 얻을 수 있도록 조각해야 합니다. 특히 사파이어나 루비처럼 색이 중요한 보석들은 광채보다 중량을 우선해, 대부분 원석의 모양에 맞춰 타원이나 사각형으로 조각합니다.
쿠키를 만들어 본 적 있나요? 넓게 편 밀가루 반죽 위에 모양틀을 도장처럼 찍으면 별, 하트 모양의 반죽이 뚝뚝 떨어져 나옵니다. 그런데 틀을 무턱대고 찍으면 안 됩니다. 반죽의 크기는 정해져 있어서 틀을 최대한 바짝 붙여 찍어야 많은 쿠키를 만들 수 있습니다. 원석에서 중량이 큰 보석을 만드는 일도 반죽을 찍는 일과 비슷합니다. 보석을 원, 타원, 브릴리언트 커트 등 어떤 모양으로 조각할지 결정했으면 원석에서 가장 큰 보석이 나오도록 위치와 방향을 잘 맞춰야 합니다.

보석계 알뜰 살림꾼, 최적화 이론
이렇게 정해진 조건 안에서 최댓값 또는 최솟값을 구하는 문제를 수학에서는 ‘최적화 문제’라고 합니다. 주어진 구간에서 함수의 최댓값과 최솟 값을 구하는 문제도 일종의 최적화 문제라고 할 수 있지요.
최적화 문제 중 조건이 무수히 많은 경우를 ‘반무한 최적화 문제’라고 하는데, 원석에서 가장 큰 보석을 조각하는 문제가 여기에 속합니다. 제멋대로 생긴 원석을 조각할 수 있는 방향이 무한개이기 때문이지요.
반무한 최적화 문제는 조건이 많기 때문에 일반적인 최적화 문제보다 풀기 어렵습니다. 학자들은 컴퓨터 알고리즘을 이용해 반무한 최적화 문제의 근사해를 찾았는데, 이 방법을 이용해 조각하자 이전에 얻었던 중량보다 더 무거운 보석을 얻을 수 있게 됐습니다. 수학 덕분에 어렵게 얻은 원석을 최대한 낭비하지 않게 된 겁니다.
보석을 조각하는 수학의 뛰어난 솜씨, 잘 감상 하셨나요? 이렇게 아름다운 보석이 만들어지는 모든 과정에는 수학의 손길이 필요합니다. 가끔은 보석의 아름다운 외모뿐 아니라 내면을 들여다보는 여유를 가져 보세요. 아름다운 보석 뒤에는 똑똑한 조각가 수학이 숨어있습니다.












