음악만 수학을 만드는 게 아니죠. 수학으로 음악을 만든 역사는 훨씬 오래 됐습니다. 클래식 음악에 기여한 수학적 작곡법부터 최신 이슈까지 살펴봅시다.
주사위만으로 음악을 만들면 어떨까. 볼프강 아마데우스 모차르트는 1792년 ‘음악적 주사위 놀이’라는 왈츠 작곡법을 발표했다. 주사위 두 개를 던져 나오는 수에 따라 모차르트가 미리 만든 176개 마디를 재배열하면 ‘음알못’도 훌륭한 곡을 만들 수 있다.
모차르트는 11×8 표 두 개와 176마디의 악보를 만들었다. 아래 악보는 176개 마디 중 처음 8개만 발췌한 것이다. 만약 처음에 주사위를 두 개 던져 합이 5가 나왔다면 첫번째 표의 (5,I )칸 속 숫자 40번에 해당하는 마디가 첫 번째 마디가 된다. 같은 방법으로 오른쪽으로 한 열씩 이동하며 주사위를 8번 던지면 총 8개 마디가 생긴다. 이 8개 마디를 똑같이 반복해 9~16번 마디를 만든다.
그 다음에는 오른쪽 표를 이용한다. 1~8번 마디를 만든 것과 같은 방법으로 오른쪽 표를 이용해 17~24번 마디를 만든 뒤 25~32번 마디는 이를 반복한다. 다음 33~48번 마디는 다시 왼쪽의 표로 작곡한다. 이처럼 확률로 만드는 음악을 ‘우연성 음악’이라 한다. 우연성 음악은 20세기 이후 현대 음악의 한 계통을 이룰 정도로 흥행했다.

도형으로도 음악을 만든다
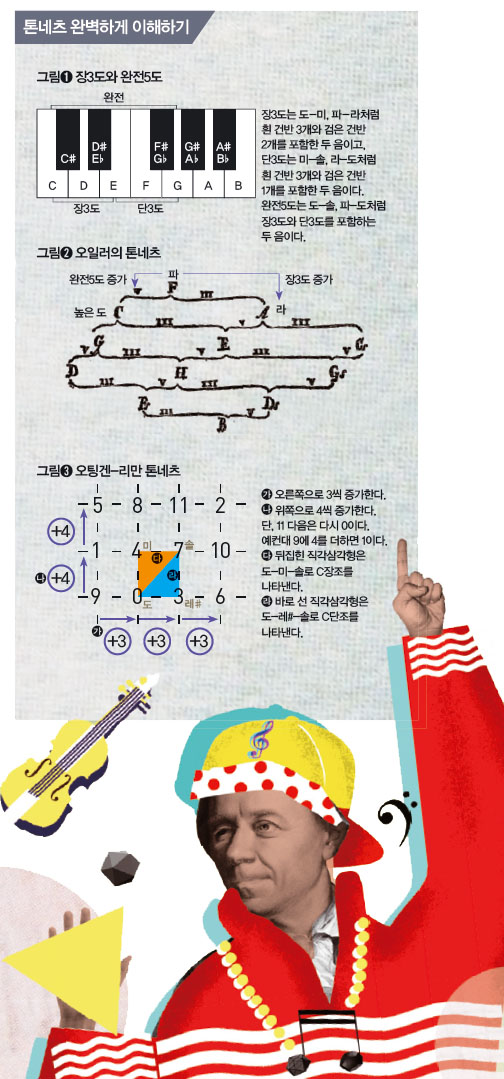
모차르트가 확률로 음악을 만들었다면 수학자 레온하르트 오일러는 1739년 도형으로 음악을 만드는 법을 제시했다. 자주 쓰는 화음을 그림으로 나타내 쉽게 화음을 만들도록 한 것이다. 오일러는 이 그림을 ‘음조 네트워크’를 뜻하는 독일어인 ‘톤네츠’라 불렀다.
그림➊에서 장3도와 완전5도를 보자. 오일러의 톤네츠만 있으면 어려워 보이는 이 음악 용어를 잘 몰라도 노래 속에 맘껏 사용할 수 있다. 그림➋에서 C, D, E, F, G, A, B는 각각 도, 레, 미, 파, 솔, 라, 시다. v는 완전5도, m은 장3도 차이를 나타낸다. 가장 위의 F에서 왼쪽의 v라 적힌 선을 따라 가면 F보다 완전5도 높은 C(높은 도)가 있다. 반대로 오른쪽 m으로 가면 F보다 장3도 높은 A가 있다. 선을 따라가며 피아노를 치면 음이 부드럽게 진행된다.
음악학자 아서 폰 오팅겐과 휴고 리만은 오일러의 생각을 오팅겐-리만 톤네츠로 발전시켰다. 이 톤네츠에 나타난 숫자는 12음계에 해당한다. 도는 0, 도#은 1, 레는 2 등으로 12음계에 0~11을 부여했다. 12개 숫자가 일정한 규칙에 따라 배열돼 쉽게 곡을 만들 수 있다.
예를 들어 그림처럼 4개의 숫자로 두 개의 직각삼각형을 만들어보자. 위쪽의 음 3개는 C장조, 아래쪽은 C단조를 이룬다. 이런 직각삼각형 쌍을 어디에서 만들든 각 삼각형을 이루는 화음은 서로 조성은 같되 위쪽은 장조, 아래쪽은 단조가 된다. 이런 성질 때문에 서양 고전 음악 작곡가들은 오팅겐-리만 톤네츠에서 만들어지는 삼각형을 위 혹은 아래, 대각선 쪽으로 한 칸씩 이동시키며 곡을 만들기도 했다.

실시간 작곡에 듀엣까지
수학으로 즉석 작곡도 가능하다. 여럿이 모여 동료의 연주를 듣고 즉흥적으로 멜로디를 만들어가며 하는 연주를 ‘잼’이라고 한다. 이런 잼 연주를 할 수 있는 인공지능이 나왔다.
2017년 2월 구글의 개발자이자 뮤지션인 요탐 맨은 사람과 잼을 하는 인공지능을 공개했다. 사람이 가상 피아노를 연주하면 인공지능도 가상 피아노로 화답한다. 가상 악기가 아니라 진짜 마림바를 연주하는 인공지능도 있다. 미국 조지아공과대학교에서 로봇 음악가를 개발하는 ‘로보틱 뮤지션십 그룹’은 실로폰의 일종인 마림바로 즉석에서 멜로디를 반주하는 로봇 시몬을 개발했다.
시리가 사람의 언어를 듣고 응답하는 것처럼 잼 하는 인공지능은 음악의 언어인 리듬과 멜로디, 화성★을 인식해 응답한다. 즉흥연주법을 배우는 과정은 평범한 기계학습 원리와 같다. 컴퓨터에게 수많은 고양이 사진을 주고 ‘고양이’라고 가르치면 자동으로 고양이 사진의 패턴을 배우는 것처럼 잼 인공지능도 잼 자료를 듣고 어울리는 연주의 패턴을 학습한다.
리듬과 멜로디, 화성★ 리듬은 음의 장단이나 강약이 반복될 때 규칙적인 음의 흐름이다. 멜로디는 하나의 음이 만드는 선율이고, 화성은 화음의 시간적 흐름이다.
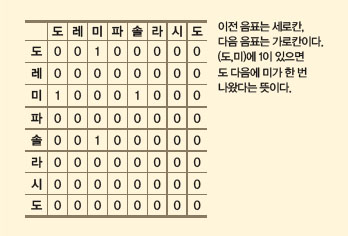
그런데 음악은 사진과 달리 시간에 따른 흐름이 중요하다. ‘도레미’와 ‘미레도’는 매우 다르기 때문이다. 따라서 컴퓨터에게 멜로디를 가르친다면 음의 순서도 함께 알려줘야 한다. 예를 들어, 도레미파솔라시도의 8음계만 연주하는 인공지능에게 ‘도미솔미도’를 가르칠 때는 위의 표를 이용한다. 이전에 나온 음 하나를 기억하는 방법이다.
창의성도 수학으로 평가한다
이렇게 만든 곡의 가치는 어떻게 평가하면 좋을까. 독일 철학자 임마누엘 칸트는 창조성의 조건으로 새로움과 본보기를 제시했다. 어떤 작품이 이전의 작품에 비해 새로울수록, 또 후대의 작품이 해당 작품을 많이 따라할수록 창의성이 높다. 이런 창의성 개념을 이용해 아흐메드 엘가말 미국 럿거스대학교 컴퓨터과학과 교수는 6만 2000점의 그림을 분석했다.
엘가말 교수는 창의성 측정 과정을 ‘네트워크 중심성 문제’로 바꾸었다. 인터넷 검색이나 전염병의 확산 경로를 분석할 때 쓰이는 문제로, 어떤 미술품이 다른 작품에 영향을 미쳤는지 알 수 있다. 엘가말 교수는 작품의 색과 질감, 대상 같은 특징을 변수로 하고 작품 간의 연관성을 조사했다.
이교구 서울대학교 융합과학기술대학원 교수는 “음악에서도 같은 방법으로 창의성을 분석할 수 있을 것”이라고 말했다. 음악의 리듬과 멜로디, 화성과 같은 주요 특징을 새로움과 본보기 지표를 기준으로 분석하면 된다는 것이다. 예술에 점점 더 가까워지는 수학과 수학에 점점 더 가까워지는 음악의 미래가 기대된다.

▼관련기사를 계속 보시려면?
Intro. 딴따라 수학과 똑똑이 음악의 듀엣 타임!
Part 1. 음악, 수학을 만들다
Part 2. 수학, 음악을 만들다











