d라이브러리

 

움빠룸빠 둠 두비두바 둠
멈추지 않아 춤을 춘다, 다시♬ 다시♬

아이유의 3집 타이틀곡 ‘분홍신’을 들어보자. 밀고 당기는 박자에 몸이 저절로 들썩인다. 이게 바로 재즈다. 아이유는 ‘분홍신’을 즉흥연주 기법으로 녹음했다. 전체 흐름만 정하고 멜로디와 박자는 연주자들이 즉석에서 만든 것이다. 이런 즉흥연주는 재즈의 핵심이다.

제멋대로인 것처럼 보이는 재즈에서 탄생한 수학 알고리즘이 있다. 김종우 가천대학교 에너지IT학과 교수는 미국 버지니아공과대학교의 방문 연구원으로 일하던 2001년 재즈의 즉흥연주를 흉내 낸 최적화 알고리즘 ‘하모니 서치’를 만들었다. 최적화 알고리즘은 어떤 범위 안에서 최댓값 또는 최솟값을 찾는 계산 모형이다.

하모니 서치가 모방한 즉흥연주의 특징은 ‘기억’이다. 재즈 연주자는 좋았던 연주를 기억했다가 즉흥연주에서 반복한다. 그러다 지루하면, 좋았던 연주를 조금 바꾸거나 완전히 새로운 연주법을 시도한다. 그중 좋은 건 다시 기억한다.

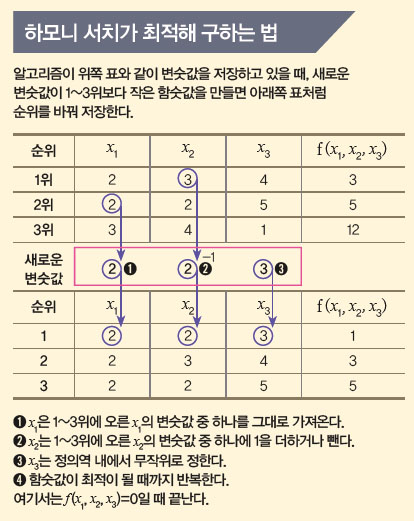
처음에는 무작위로 변수에 수를 넣어 함숫값이 작은 순서대로 순위를 매긴다. 왼쪽의 표처럼 3위까지만 저장한다고 하자. 이제 표에 나타난 방법을 이용해 새로운 변숫값을 정한다. 그 결과 함숫값이 3위보다 작게 나오면 순위를 바꾼다. 이 과정을 반복하면 최적해에 가까운 변숫값을 구할 수 있다. 표에서는 세 가지 방법을 모두 한 번씩 사용했지만, 실제로는 각 방법을 사용하는 비율을 달리하며 더 쉽게 최적해를 찾는다.

 

계산이 지나치게 오래 걸리는 문제나 답을 찾는 방법이 밝혀지지 않은 복잡한 문제를 풀기 위해서다. 하모니 서치와 같은 최적화 기법은 정확한 답을 구하기 어려운 문제의 답을 최대한 비슷하게 구하게 해준다. 생물의 진화를 모방한 유전 알고리즘이 1970년 등장한 이후, 하모니 서치처럼 인간과 자연 현상을 흉내 낸 최적화 기법이 여럿 나타났다. 건물을 짓고 상수도 망을 건설하는 실생활 문제를 풀기 위해서다.

하모니 서치를 만든 김 교수도 토목공학을 전공했다. 클래식 음악 잡지에 글을 실을 정도로 음악을 좋아하다 토목 분야의 최적화 문제를 풀기 위해 재즈를 응용했다. 김 교수는 “대학원 시절 활동하던 합창단에서 만난 수학과 교수님과 재즈과 교수님의 도움을 받았다”고 말했다.


지하와 우주로 울려퍼지다
음악은 어디까지 영향을 미칠까. 하모니 서치를 처음 제안한 2001년의 논문은 현재까지 3000여 회 인용되며 토목과 건축, 도시설계와 천문학 등 다양한 분야에서 쓰였다.

 상수도 

지하에서 옥상까지 물을 올려라!
상수도관은 강한 압력으로 높은 곳까지 물을 충분히 보내야 한다. 관의 지름을 늘리거나 펌프를 설치하면 물의 양과 압력을 높일 수 있다.

그런데 지름이 긴 관은 설치비용이 높지만 유지비용이 낮은 반면 펌프는 반대다. 따라서 관 지름과 펌프 세기가 적절해야 비용이 적게 든다. 하모니 서치는 여러 지점의 상수도관 지름과 펌프의 세기를 변수로 두고 비용을 최소로 하는 최적해를 찾는다.

 자율주행자동차 

사람 없는 자동차에게 길을 알려라!
자율주행자동차는 3차원 공간을 2차원 평면에 놓을 때 모든 선이 향하는 점인 소실점으로 차선을 찾는다. 모든 선을 소실점과 연결했을 때 특정한 각도를 이루는 선의 쌍들이 차선이다.

소실점은 영상 속 모든 선분을 연장해 교점을 구하면 된다. 실제로는 모든 직선이 한 점에서 만나지 못하기 때문에 김 교수는 하모니 서치로 모든 직선에서 거리가 가장 짧은 점을 계산해 소실점을 찾는 법을 연구하고 있다.

 외계행성 

우주에서 제2의 지구를 찾아라!
하모니 서치는 외계행성을 찾는 데도 쓰였다. 유럽우주국이 2010년 지구에서 1500광년 떨어진 곳에 있는 행성 ‘CoRoT-9b’를 발견했을 때다.
◀ CoRoT-9b가 모항성 앞을 지날 때 모항성의 빛을 가리는 모습을 표현한 이미지.

연구팀은 이 행성이 항성을 지나갈 때 항성의 빛을 일부 막는 현상을 이용했다.

망원경이 인식하는 빛 신호는 오차 때문에 위아래로 요동친다. 연구팀은 실제 빛의 함수를 추정하기 위해 하모니 서치로 신호값과 함숫값의 차이를 최소화하는 함수를 구했다.
 

 

서로 도우며 최적을 찾는다
음악을 좋아하는 수학자와 과학자는 더 있다. 2012년 라미레즈 로드리게즈 자비에 멕시코 자치대학교 시스템학과 교수는 작곡하는 과정을 모방해 ‘음악적 작곡법(MMC)’이라는 최적화 알고리즘을 만들었다.

바이올린을 사랑하는 진 하디스티. ▶
 

자비에 교수는 작곡가가 혼자서가 아니라 다른 작곡가와 소통하며 창작 활동을 한다고 봤다. 그래서 자기 경험에 따라 작곡을 하기도 하지만 동료 작곡가에게 새로운 정보를 얻어 더 좋은 곡을 만들기도 한다. 스스로 작곡하는 것과 정보의 교환이 반복되면서 음악적 작곡법 알고리즘은 최적해를 찾는다.

바이올린을 좋아하는 진 하디스티는 미국 라이스대학교 응용수학과에서 박사 후 연구원으로 일하던 2013년 최적의 바이올린 모양을 찾는 수학적 방법을 제시했다. 바이올린의 모양을 나타내는 복잡한 방정식을 쉽게 푸는 해법을 찾은 것이다. 이 해법은 악기 제작뿐만 아니라 빛의 움직임에 대한 문제에도 적용할 수 있다. 예를 들어 전투기가 빛을 반사해 적에게 노출될 가능성을 줄이기 위한 최적의 전투기 모양을 찾는 데 쓰인다.



▼관련기사를 계속 보시려면?

Intro. 딴따라 수학과 똑똑이 음악의 듀엣 타임!
Part 1. 음악, 수학을 만들다​
Part 2. 수학, 음악을 만들다​