d라이브러리 2011년 12월 수학동아

스마트폰을 처음 사면 가장 먼저 뭘 하나요? 아마 기본적인 설정을 하면서 배경화면을 잠그는 암호를정할 거예요. 제가 만든 스마트폰은 숫자 4자리로 된 암호를 씁니다. 0000부터 9999까지 암호를 만들수 있어 경우의 수는 총 1만 개지요. 생각보다 원리가 간단한가요?
말했잖아요. 저는 간단한 걸 좋아한다고요! 그런데 경쟁사의 스마트폰은 패턴암호라는 독특한 암호를 씁니다. 그 원리를 알아볼까요?

패턴암호 경우의 수 구하기

스마트폰은 기계마다 사용하는 운영체제가 다르다. 그 중 구글에서 만든 안드로이드체제를 사용하는 스마트폰에서는 숫자 비밀번호 외에도‘패턴암호’를 사용할 수 있다. 이 암호는 9개의 점을 지나며 그린 패턴을 암호로 쓴다. 그렇다면 패턴암호의 경우의 수는 얼마나 될까? 먼저 패턴암호의 경우의 수를 구하려면 조건을 정확하게 알아야 한다.

스마트폰은 운영체제에 따라 배경화면 암호로 4자리 숫자(왼쪽)나 패턴암호(오른쪽)을 쓴다.

패턴암호 조건

❶ 점은 최소 4개부터 최대 9개까지 지날 수 있다.
❷ 같은 숫자(점)를 두 번 지날 수 없다. 예를 들어 1→2→3→5→1은 될 수 없다.
❸ 같은 패턴이더라도 시작점이 다르면 다른 암호다. 예를 들어 1→4→5→6과 6→5→4→1은 모양은 다르지만, 시작한 숫자가 다르므로 다른 암호다.

이제 경우의 수를 구해 보자. 먼저 각 숫자에서 선을 그릴 수 있는 숫자와 그릴 수 없는 숫자가 있다는 걸 생각해야 한다. 예를 들어 1이란 숫자에서는 2, 4, 5, 6, 8로 선을 그릴 수 있지만 3, 7, 9로는 그릴 수 없다. 그 사이에 2, 4, 5란 숫자가 끼어 있기 때문이다.

그림❶

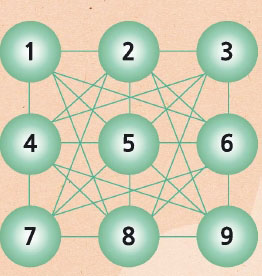
따라서 각 숫자에서 그릴 수 있는 숫자로 선을 이으면 그림❶과 같은 그래프가 된다. 각 숫자에서 그을 수 있는 선을 비교해 보면 정사각형 모서리에 있는 숫자 1, 3, 7, 9에서 그을 수 있는 선의 개수는 5개, 변에 있는 숫자 2, 4, 6, 8은 7개, 한 가운데 있는 5는 그을 수 있는 선의 개수가 8개다.

그림❷

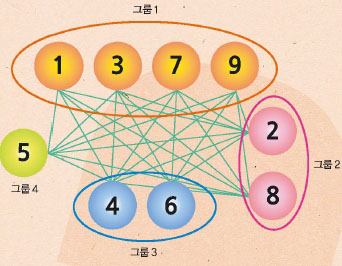
여기서 문제를 해결하기 쉽도록 숫자의 위치를 바꿔 그림❷와 같이 다시 배열한다. 그래프는 점의 개수와 연결된 선의 개수만 바뀌지 않는다면 위치를 바꾸는 것은 문제되지 않는다. 그런 다음 연결할 수 있는 선의 개수에 따라 그룹1부터 그룹4까지 묶는다.

여기서 연결할 수 있는 선의 개수가 같음에도 불구하고, 2, 4, 6, 8을 두 그룹으로 나눴다. 그룹 안의 숫자는 바로 선을 그을 수 없다는 공통적인 성질을 유지하기 위해서다. 2, 4, 6, 8을 한 그룹으로묶으면 2와 4는 선을 바로 그을 수 있지만, 2, 8을 그룹2로, 4, 6을 그룹3으로 나누면 모든 그룹은 그 안의 숫자가 바로 그을 수 없는 숫자들로 이뤄진다.

이렇게 그룹을 나눈 다음, 각 그룹에서 숫자를 선택해 패턴의 경우의 수를 구한다. 패턴암호에 따라 최소 4개의 점을 지나는 패턴부터 최대 9개의 점을 지나는 경우까지 나눈다. 패턴의 길이(지나는 점의 개수)가 4인 경우부터 각각을 계산해 보면 1400가지, 5184가지, 16032가지, 35328가지, 49536가지,32256가지가 나온다. 모두 더하면 139736가지로, 패턴암호로 만들 수 있는 암호는 숫자 4개로 만들 때보다 무려 10배 이상 많다.

경우의 수가 무한한 암호도 있다!

숫자 비밀번호와 패턴암호는 모두 경우의 수를 정확히 계산해 구할 수 있다. 그러나 경우의 수가 무한한 암호도 있다. 이 암호는 손가락으로 자신이 그린 그림을 암호로 쓴다. 원리는 간단하다. 기계는화면을 조밀한 모눈종이로 나눠 인식한다. 사용자가 그린 그림에 해당하는 칸을 선택하면 같은 암호로 받아들인다. 화면을 나누는 칸이 많을수록 암호의 보안성은 높아진다. 하지만 단점이 있다. 그린 모양을 정확히 기억하지 못하면 자신이 걸어 놓고도 암호를 풀지 못할 수도 있다는 것!

경우의 수가 무한한 암호도 있다!

d라이브러리

Part 1. 패턴암호 경우의 수는 몇 개일까?