d라이브러리

뫼비우스 띠가 180°로 한 번 꼬아서 양 끝을 붙인 거라고 하면, 두 번, 세 번 꼬인 횟수를 늘려 가면 이것 또한 뫼비우스 띠일까? 그 답은 도형의 연결 상태에 있어.

도형을 구분하는 두 번째 기준, 연결상태

찰흙으로 만든 정육면체를 생각해 봐. 찰흙을 떼어 내지 않고 늘이거나 뭉치면서 구를 만들 수 있지? 사각뿔도 만들 수 있을 거야. 위상수학자들은 이렇게 만든 두 도형을 구분하지 않아. 모두 같다고 생각하는 거지. 도형의 점, 선, 면의 위치 관계에만 관심이 있기 때문이야. 조금 어렵게 말하자면 위상이 같다고 말할 수 있어.

연결상태가 같은 도형 - 선
 

첫 번째 도형을 자르지 않고 모양만 바꿔 두 번째, 세 번째 도형을 만들 수 있다.

연결상태가 같은 도형 - 면
 

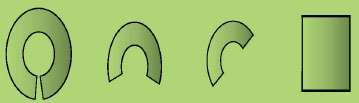
첫 번째 도형을 적당히 펴서 늘이면 직사각형을 만들 수 있다.

연결상태가 같은 도형 - 입체
 

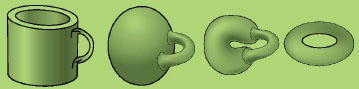
컵을 도넛 모양으로 바꾸는 과정이다. 컵 부분을 뭉치면, 구가 된다. 구를 소세지 모양처럼 주무르다가 도넛을 만들 수 있다. 도넛과 컵은 위상이 같은 도형이다.

처음 질문으로 돌아가 볼까? 직사각형 모양의 띠를 180° 만큼 홀수 번을 꼬아서 이으면 뫼비우스 띠와 연결상태가 같아. 이들 도형 위에서 점, 선, 면의 위치관계는 같지. 180° 만큼 짝수 번 꼬면 이 도형들은 생긴 건 달라도 원통형 띠와 성질이 같아. 뫼비우스 아저씨는 아마 홀수 번 꼰 띠를 구별하지 않고 모두 뫼비우스 띠라고 말할 거야. 자세한 건 수학동아 홈페이지(math.dongascience.com)를 참조해 봐! 재미있는 실험도 함께 보여 줄 테니까.

도형을 구분하는 세 번째 기준, 면의 개수

클라인 병과 구, 도넛, 구멍이 두 개인 도넛은 모두 입체 도형이야. 그런데 이 네 도형은 무엇이 다를까? 도형을 이루는 면의 개수로 클라인 병과 나머지 도형을 나눌 수 있어. 클라인 병은 안과 밖의 구분이 없는 면이 한 개인 도형이지만 구, 도넛, 구멍이 두 개인 도넛은 면이 두 개로 안과 밖을 구분할 수 있어. 구멍이 두 개인 도넛은 도넛 두 개를 연결한 모양인데, 여러 개의 도넛을 붙여 구멍이 여러개 나와도 언제나 면의 개수는 두 개야. 이 성질은 변하지 않지.

도형을 구분하는 기준이 이게 전부는 아니야. 곡면의 성질 등 이 밖에도 여러 가지 기준으로 도형을 성질을 알아 내고 다시 분류해. 도형의 성질을 잘 알면 화학, 건축 등 다른 분야에서 응용할 수 있는 기회도 많아.

앞으로 찰흙 놀이를 하면서도 위상수학자처럼 생각해 보는건 어때?

도넛 지갑을 만들어 보자!
 

기분에 따라 바꿔 쓸 수 있는 도넛 지갑을 만들자! 두 면을 갖는 도넛의 성질을 이용해 양면 지갑을 만들 수 있다. (자세한 순서는 홈페이지를 참고 하세요.)

➊ 적당히 큰 정사각형의 천을 접는다.
➋ 만나는 모서리를 실로 꿰맨다.
➌ 반대로 뒤집어 그림과 같이 접는다.
➍ 안쪽 면만 이음새를 실로 꿰매면 도넛 지갑 완성. 입이 세로로 벌어진다.
➎ 완성된 지갑을 뒤집는다.
➏ 지갑의 입이 가로로 벌어지면서 새로운 면이 나온다.

뫼비우스 실험실

뫼비우스 아저씨와 앤츠가 함께하는 신기한 수학 실험실에 온 걸 환영해! 뫼비우스 아저씨를 따라 뫼비우스 띠도 직접 만들어 보고 이 앤츠가 내는 문제도 풀어 봐. 실험이 끝난 뒤엔 바로 퀴즈를 낼 거니까 계속 긴장하고 있어야 해~.

실험1 두 개의 띠가 있어. 각각의 도형에서 가운데 선을 따라 자르면 나오는 결과는 같을까 다를까?
 

결과 뫼비우스 띠의 양쪽 끝은 서로 다른 면과 붙고, 원통형 띠는 같은 면끼리 붙지. 첫번째 결과는 놀랍게도 사각형이 나왔어. 그럼 두 번째 띠를 자른 결과는 어떨까? 궁금하겠지만, 직접 만들어 보고 ‘수학동아로 모여봐’의 ‘사진을 찍어봐’ 코너에 보내 줘.

실험2 이번 실험은 서로 반대방향으로 꼰 뫼비우스 띠 두 개가 필요해. 이번에도 두 개의 띠를 수직으로 붙여 가운데 선을 따라 자르면 어떤 모양이 나올까?
 

결과 서로 연결된 예쁜 하트가 나와. 사랑을 전하는 뫼비우스 띠~, 신기하지?

앤츠와 함께 하는 퍼즐!

1 길이가 20cm인 띠로 만든 뫼비우스띠 위를 무당벌레가 기어 가고 있다고 상상해 봐. 무방벌레가 처음 위치로 돌아왔다면 무당벌레가 돌고 온 총 거리는 얼마일까?
 

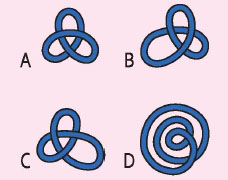
2 다음과 같이 원 모양의 고리가 있어. 다음 네 개의 띠 중에서 원 모양의 고리와 다른 것을 찾아 볼래?
 

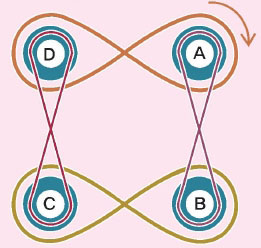
3 네 개의 원판에 고리가 걸려 있어. A판이 시계방향으로 돌 때, C판은 어느 방향으로 돌까?
 

4 길이가 20cm인 띠로 180° 만큼 두번 꼰 종이를 만들었어. 이 위를 무당벌레가 기어서 처음 위치로 돌아온다면 무당벌레가 돌고 온 총 거리는 얼마일까?



▼관련기사를 계속 보시려면?

뫼비우스 행성 탐험기
첫째 날 M-214호에 떨어지다
둘째 날 알쏭달쏭 신기한 세계
셋째 날 상상하면 이뤄질까?
마지막 날 현실과 통하는 문, 클라인 병 건물로!
뫼비우스 띠, 위상수학 돋보기로 다시 보자!
도넛과 머그컵이 똑같이 생겼다고?