
따르릉~. 수학 시간이 시작됐다. 수학 공부를 하기 위해 책상 위에 준비물을 꺼내 본다. 종이, 연필, 각도기, 자 등등…. 그런데 옆자리 친구는 달랑 종이 한 장만을 꺼내 놓고는 가만히 있는 게 아닌가. 안 가져왔으면 빌려 줄까 싶어서 묻자 친구가 씨익- 웃으며 대답한다.“난 종이 한 장이면 충분해~!”종이 한 장이면 충분하다고? 도대체 종이만 갖고 뭘 하겠다는 거지?
종이접기로 수학 문제를 푼다?!
종이를 곱게 접어 만든 학 천 마리를 예쁜 병에 담으면 감동적인 선물이 된다. 예쁜 꽃을 만들어 머리에 꽂을 수도 있다. 아니면 통통 튀는 개구리를 만들어 친구들과 가지고 놀 수도 있다. 그런데 종이를 가지고 수학 문제를 풀 수 있다는 건 무슨 소리일까?
종이접기는 종이가 발명된 고대에 시작되었다. 하지만 오늘날 우리가 접하는 현대식 종이접기는 1700년대 일본에서 발달하기 시작한 이후 수학의 한 분야로 발전하기에 이르렀다. 세계적으로 많은 수학자가 종이접기의 수학을 연구한 끝에 현재는 종이접기를 이용해 4차 방정식까지 풀 수 있는 수준까지 발전했다. 방정식 외에도 변의 비가 황금비를 이루는 ‘황금 사각형’이나 다양한 다각형을 접을 수 있어 기하학을 공부하는 데 큰 도움이 된다. 무엇보다 손쉽게 구할 수 있고 직접 만들어 보는 체험을 할 수 있다는 것이 가장 큰 장점! 그러면 종이접기의 능력을 맛보기 전에 종이접기의 기본 공리를 살펴보자.
종이접기의 기본 공리
1991년 일본의 수학자 후미아키 후지타는 종이접기에 관한 국제회의에서 종이접기의 기본 공리를 발표했다. 후지타가 발표한 6가지의 공리는 종이접기의 기본적인 바탕이 되는 원리다. 직접 종이를 들고 종이접기의 공리를 몸으로 느껴 보자.
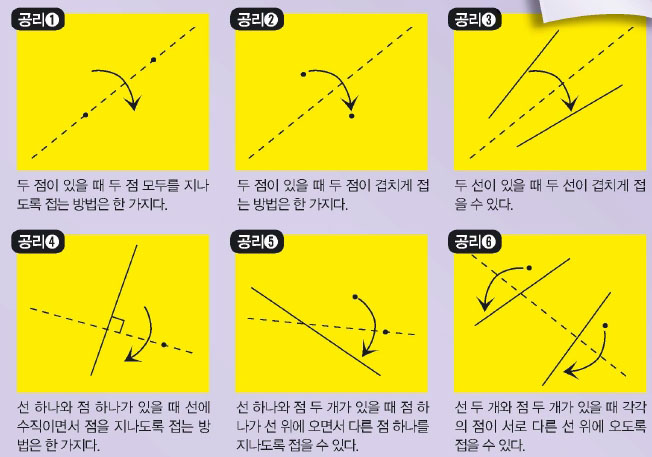
종이만 있으면 계산이 술술
종이접기를 이용해 곱셈과 나눗셈을 해보자. 종이접기로 곱셈과 나눗셈을 할 때 이용하는 원리는 닮음이다. 서로 모양이 같고 크기가 다른 두 도형의 크기 비율을 이용해 두 수를 곱하거나 나눌수 있다. 함께 따라해 보자.

곱셈 : 3X2를 할 때

원리
순서에 따라 종이를 접으면 삼각형이 두 개 생긴다. 이 삼각형 OAU와 삼각형 OBP는 서로 닮음이다. 따라서 O에서 U까지의 거리와 O에서 A까지의 거리의 비는 O에서 B까지의 거리와 O에서 P까지의 거리의 비와 같다. OU는 1이고 OA는 3, OB는 2이므로 1:3=2:OP가 된다. 1×OP=3×2이므로 OP=6이 된다.
나눗셈 : 4÷2를 할 때

원리
삼각형 OAB와 삼각형 OUQ는 서로 닮음이므로 OU:OQ=OB:OA가 된다. OU는 1이고 OA는 4, OB는 2이므로, 1:OQ=2:4. 따라서 OQ=2가 된다.

접으면 쉽다~
종이를 똑같은 길이로 나누고 싶을 때는 어떻게 해야 할까? 짝수 등분이라면 절반씩 나눌 수 있겠지만, 홀수 등분이라면 변의 길이를 자로 재고 나누고 싶은 수로 나눠서 간격을 계산해야 해 불편하다. 하지만 종이접기를 이용한다면 자나 컴퍼스가 없어도 종이를 똑같이 나눌 수 있다. 이처럼 종이접기를 이용하면 어려운 문제를 쉽게 해결할 수 있다.
종이를 7등분 하기

원리
종이를 8등분하는 선은 모두 서로 평행하다. 따라서 사각형의 두 변과 평행선이 만드는 삼각형은 모두 닮음이다. 평행선 사이의 간격이 일정하므로 삼각형의 닮음비는 일정하다. 삼각형 ABC와 ADE의 닮음비는 1:2가 되기 때문에 선분 AB와 AD의 비도 1:2가 된다. 즉 선분 AB의 길이는 선분 BD의 길이와 같다. 마찬가지 방법으로 계산하면 사각형의 변을 나누는 각 선분의 길이는 모두 같다.
종이 위에 원이 있을 때 중심점을 알아 내려면 어떻게 해야 할까? 어림짐작으로 중심점을 찍을 수는 있지만 정확하게 알아 내기는 어렵다. 자와 컴퍼스로 여러 차례 선을 그으면 구할 수 있지만, 종이접기를 이용하면 4번 만에 원의 중심점을 구할 수 있다.
원의 중심 알아내기

원리
원의 중심을 M이라고 하면 삼각형 ABM은 A와 B가 겹치도록 접었을 때 완전히 포개지는 이등변삼각형이다. 따라서 선분 AM과 선분 BM의 길이가 같다. 삼각형 ACM도 A와 C가 겹치도록 접었을 때 완전히 포개지는 이등변삼각형으로, 선분 AM과 선분 CM의 길이가 같다. 따라서 선분 AM과 선분 BM과 선분 CM의 길이는 모두 같다. 이 때 M을 중심으로 반지름의 길이가 선분 AM과 같은 원을 그리면 점 A, B, C를 모두 지나는 원이 된다.
안 되는 것을 되게 한다
수학에는 고대 그리스 시대부터 내려온 3대 작도 불가능 문제가 있다. 즉, 자와 컴퍼스를 이용한 작도로는 절대 그릴 수 없다고 알려진 문제다. 오랜 시간 동안 많은 수학자들이 풀이법을 알아 내려고 노력했지만 성공하지 못했고, 결국 19세기에 들어서야 불가능하다는 사실이 증명됐다. 하지만 종이접기를 이용하면 이 3대 작도 불가능 문제 중에서 2가지를 해결할 수 있다. 안 되는 것을 되게 하는 종이접기의 능력을 살펴보자.
임의의 각을 3등분하라
3대 작도 불가능 문제 중 첫 번째는 ‘임의의 각을 3등분하는 문제’다. 직각을 비롯한 일부 각은 작도로 3등분하는 게 가능하지만, 무작위로 어떤 각이 주어졌을 때 작도로 3등분할 수 있는 방법은 없다는 뜻이다. 19세기에 프랑스의 수학자 피에르 반첼은 이 문제를 작도로 푸는 게 불가능하다는 사실을 증명했다. 하지만 다음과 같이 종이를 접으면 접힌 선이 각을 삼등분하도록 만들 수 있다.
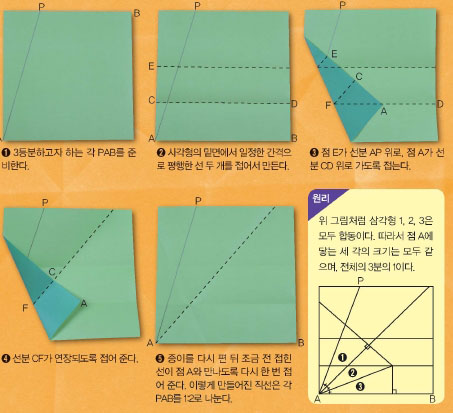
원리
위 그림처럼 삼각형 1, 2, 3은 모두 합동이다. 따라서 점 A에 닿는 세 각의 크기는 모두 같으며, 전체의 3분의 1이다.
부피가 2배인 정육면체 만들기
‘어떤 정육면체가 있을 때 부피가 2배인 정육면체를 작도하는 문제’는 흔히 ‘델로스의 문제’라고도 부른다. 전설에 따르면 아폴로 신이 고대 그리스의 델로스에 전염병을 퍼뜨리자 시민들은 신관에게 어떻게 해야 할지 물었다. 그러자 신관은 아폴로 신에게 바치는 제단의 크기를 2배로 만들면 된다고 했다. 이에 시민들이 정육면체 모양인 제단의 각 변을 2배씩 늘려 새 제단을 만들었다. 하지만 전염병은 수그러들지 않았다. 왜냐하면 아폴로 신은 부피가 2배인 제단을 원했던 것이다.
정육면체의 부피는 한 변의 길이의 세제곱이므로 각 변을 2배씩 늘리면 부피는 8배가 된다. 이 문제를 해결하기 위해서는 세제곱했을 때 원래 변의 길이의 2배가 되는 변의 길이를 알아야 한다. 작도로는 이 비율을 만들 수 없지만 종이접기를 이용하면 가능하다.
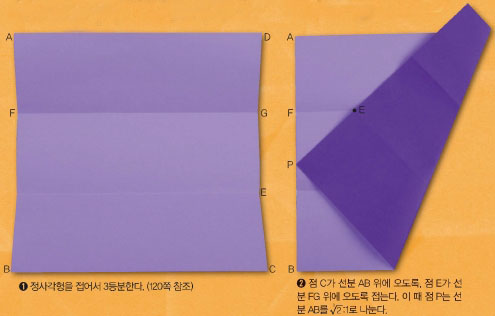
원리
x의 길이는 y의 길이의 ∛2배다. 따라서 한 변의 길이가 x와 y인 정육면체를 만들면 부피의 비가 2:1인 정육면체를 만들 수 있다.
단순한 흥밋거리로만 생각했던 종이접기에 이런 능력이 숨어 있었다니! 옆자리 친구의 자신만만한 표정이 이제 이해가 된다. 종이접기는 직접 해 볼 수 있기 때문에 도형을 이해하는 데 아주 유용하다는 친구의 설명. 좋아, 이제 연필과 자는 안녕~. 우리도 함께 종이접기로 공부해 보자고~

▼관련기사를 계속 보시려면?
썰매 삼총사와 스키 패밀리
썰매 삼총사의 달리기
뼈대있는 스키 가족
멋쟁이 스키 친척
스키, 하늘을 날다
종이접기의 재발견











