벡터 공간까지 범위를 넓히다! 로타의 추측
놀랍게도 연관성이 없어 보이는 다른 조합론 문제에서도 로그-오목이 나타납니다. 유한 차원 벡터 공간에 영벡터가 아닌 유한개의 벡터들의 집합 E가 주어지면 원소가 i개인 E의 부분 집합 중 일차독립인 것의 개수를 나타내는 수열 fi(E)를 생각할 수 있습니다. 여기서 일차독립이란 한 벡터가 나머지 벡터의 일차결합으로 만들어 질 수 없는 경우를 말합니다. 이때 E의 성질을 나타낸 특성 다항식을 정의할 수 있는데, ‘메이슨-웰시의 추측’은 특성 다항식의 계수들이 즉, 수열 fi(E)가 로그-오목인지 묻는 것입니다.
또 1935년 휘트니는 그래프와 벡터들의 집합의 공통 특성을 추상화해 ‘매트로이드’라는 개념을 도입했습니다. 유한집합 E에 매트로이드 M이 주어지면 제거-축약 공식과 초기 조건으로부터 특성 다항식을 정의할 수 있는데요. ‘로타의 추측’은 리드-호가의 추측과 메이슨-웰시의 추측을 임의의 매트로이드 M에 대해 특성 다항식의 계수들이 로그-오목임을 보이는 문제입니다.
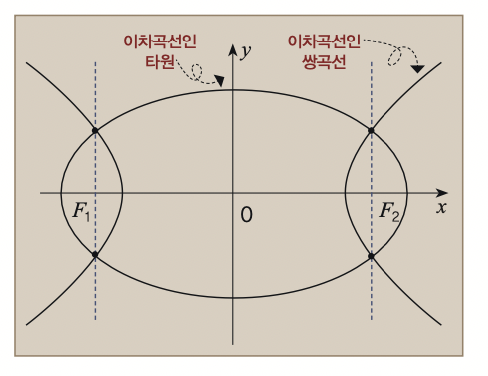
허 교수는 ‘교차수’의 재밌는 성질인 ‘호지-리만 관계’를 통해 로타의 추측이 참이라는 것을 증명했습니다. 여기서 교차수란 공간에서 다양체들이 몇 개의 점에서 만나는지를 나타낸 것입니다. 예를 들어 이차곡선과 이차곡선은 일반적으로 4개의 점에서 만나는데 이때 두 곡선의 교차수가 4입니다.
허 교수 연구의 중요성
허 교수는 조합론적으로 정의된 교차이론을 개발해 매트로이드 연구의 새 장을 열었습니다. 따라서 조합론 측면에서는 너무도 자명합니다. 그래프나 매트로이드가 왜 중요하냐고 묻는 것은 인공지능 연구에서 행렬이 왜 필요하냐고 묻는 것과 같은 우문입니다. 매트로이드의 응용 분야는 정보통신, 반도체 설계, 교통, 물류, 기계학습, 통계물리 등 셀 수 없이 다양합니다. 따라서 그래프와 매트로이드에 관한 연구는 큰 파급 효과를 가질 수밖에 없습니다.
역으로 대수기하학의 관점에서도 충격적인데, ‘사영다양체’를 거치지 않고 매트로이드에서 바로 사영다양체의 교차이론에서 나오는 고유의 성질들을 확립한 것은 현재의 대수기하학의 토대를 더욱 확대할 수 있음을 이야기합니다. 비유하자면 화성(조합론, 매트로이드)에서 얼음(호지-리만 관계)을 발견한 것인데, 이는 화성에도 생명체(기하학 구조)가 존재 가능함을 암시합니다.
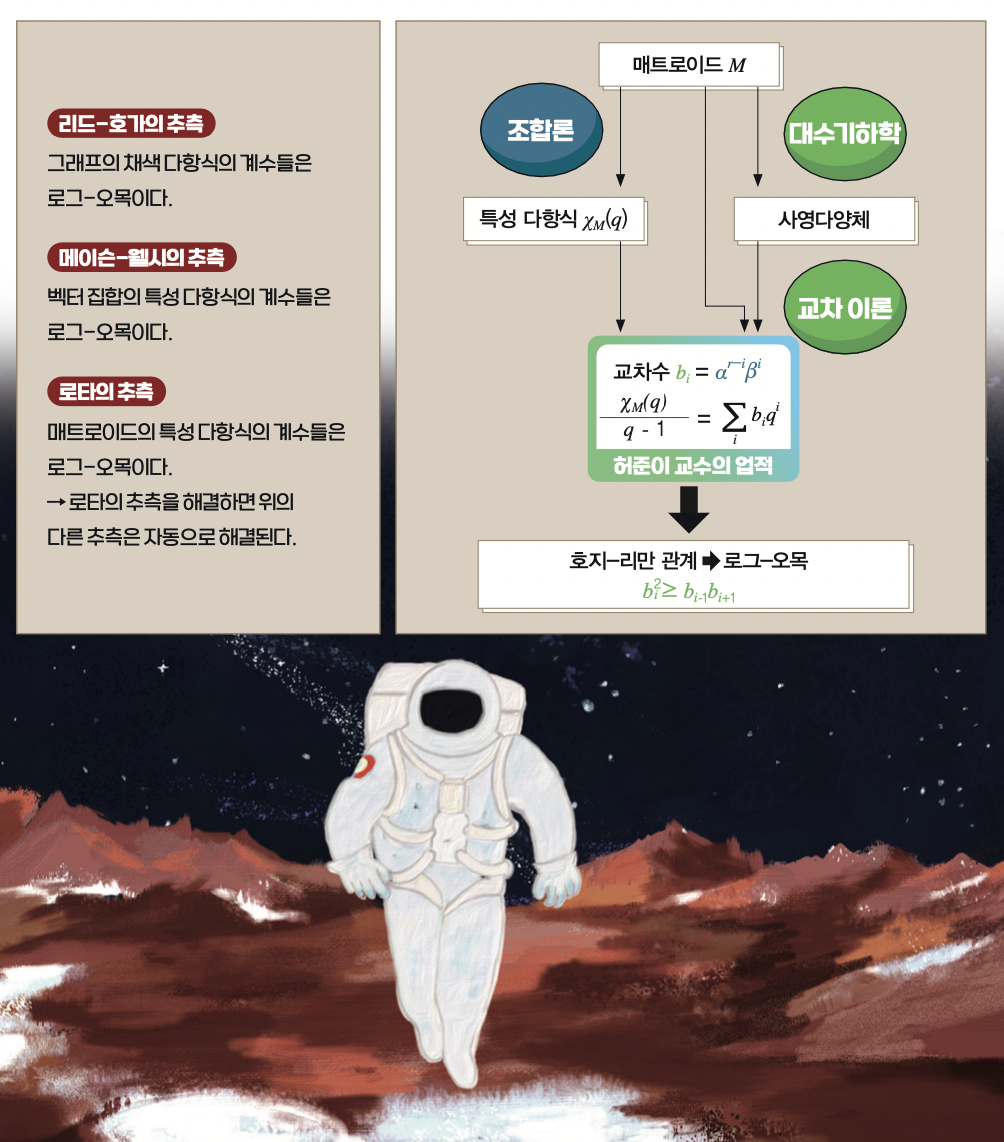
도식으로 보는 허준이 교수의 연구 성과
아래는 허 교수의 업적을 설명하는 도식입니다. 허 교수는 매트로이드로부터 사영다양체를 만들었고, 매트로이드의 특성 다항식의 계수가 사영다양체의 교차수와 같음을 증명했습니다. 이것이 허 교수의 혁명적인 아이디어입니다. 그러면 그 교차수의 호지-리만 관계가 로그-오목임이 밝혀집니다. 허 교수는 여기서 한 걸음 더 나아가 사영다양체를 거치지 않고도 특성 다항식의 계수들이 로그-오목이 됨을 증명했습니다.