d라이브러리

 

더운 여름이 지나고 풍성한 수확의 계절 가을이 성큼 다가왔다. 벌써부터 마트에선 올해 재배한 사과와 배를 싸게 팔기 시작했다. 사과를 좋아하는 경제는 마트에서 사과를 잔뜩 사서 먹기 시작했다. 1년 내내 기다린 제철 사과가 아닌가! 하지만 한 개, 두 개를 먹을 땐 맛있던 사과가 세 개, 네 개를 넘어가니 맛이 없어졌다. 세 번째, 네 번째 사과가 맛이 없었던 걸까? 아니다. 많이 먹으면 먹을수록 물리기 시작한 것이다. 이처럼 사과를 무턱대고 많이 먹을 수 없는 데에도 수학적, 경제적 이유가 있다.

다이아몬드와 공기, 어떤 것이 가치 있을까?

영화 <;도둑들>;은 다이아몬드 ‘태양의 눈물’을 훔치기 위해 한 팀이 된 한국과 중국의 도둑 10명이 펼치는 범죄 액션 드라마다. 영화에서 ‘태양의 눈물’ 하나의 가격은 무려 2000만 달러로, 한국 돈으로 따지면 200억 원 이상이다. 실제로 지금까지 가장 비싸게 팔린 다이아몬드는 2010년 미국 소더비 경매에서 약 520억 원에 낙찰된 핑크 다이아몬드다. 그야말로 어마어마한 가격이 아닐 수 없다.

그런데 이렇게 비싼 다이아몬드와 공기 중 실제 어떤 것이 우리 생활에 더 필요할까? 다이아몬드는 탐나고 비싼 물건이지만, 없어도 살 수 있다. 그런데 공기가 없으면 살 수 없다. 생존의 관점에서 보자면 다이아몬드보다 공기가 더 가치가 있다. 이상하지 않은가? 우리가 살아가는 데에는 공기가 더 중요한데, 값은 다이아몬드가 더 비싸다니!

19세기 경제학자들은 공기보다 다이아몬드가 비싼 이 현상을 ‘가치의 역설’이라고 이름 붙이고, 이를 해결하기 위해 골머리를 썼다. 그리고 ‘한계효용’이라는 개념을 도입해 이 문제를 해결했다.

한계효용은 재화나 서비스를 하나 더 이용할 때 각자가 느끼는 효용(만족)을 말한다. 다이아몬드는 귀하지만 이를 원하는 사람이 많아, 다이아몬드를 하나 더 가질 때 얻는 만족이 크다. 그러므로 다이아몬드의 한계효용은 크다고 할 수 있다. 이런 이유로 다이아몬드를 사고자 하는 사람은 많은 돈을 내고서라도 사려고 한다.

하지만 공기는 다르다. 공기를 마시는 사람들이 이미 많은 공기를 갖고 있기 때문에 더 갖는 것에 큰 만족을 느끼지 않는다. 물론 깊은 물속이나 우주에서 헤엄치고 있는 사람이라면 엄청난 돈을 내서라고 공기를 갖고 싶겠지만, 일반적으로는 돈을 내지 않는다. 따라서 공기의 한계효용은 다이아몬드보다 작아 가격도 싸다.

비빔면, 몇 개까지 먹을 수 있니?

그런데 재화나 서비스를 한 번 더 이용하면 각자가 느끼는 만족은 점점 줄어든다. 이를 가리켜 ‘한계효용 체감의 법칙’이라고 한다.

예를 들어 배고플 때 비빔면을 먹는다고 생각해 보자. 처음 비빔면 한 개를 먹을 때는 상당히 맛있다. 비빔면의 양은 1인분보다 조금 작으니 두 개째도 맛있게 먹을 수 있지만, 처음 한 개 먹을 때만은 못하다. 하지만 세 개째라면 어떨까? 배가 불러 더 이상 먹을 수가 없으니, 억지로 먹게 돼 맛을 거의 못 느낄 것이다. 만족감이 거의 없게 되는 것이다.

그렇다면 마지막으로 네 개째를 먹으면 어떨까? 이제는 먹을 수가 없어 거의 고문이라고 느낄 것이다. 급기야 만족감이 줄어든 것이다. 하나를 더 먹을수록 한계효용은 점점 줄어드는 현상을 설명한 것이 바로 ‘한계효용 체감의 법칙’이다. 이 법칙은 독일의 경제학자 허만 고센이 발견해, ‘고센의 제1법칙’이라고도 불린다.

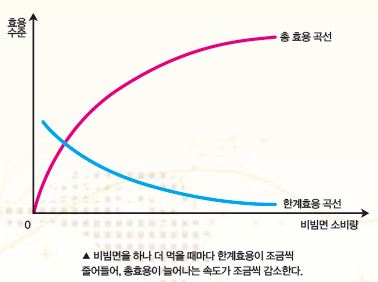
이를 그래프로 표현하면 아래와 같다. 비빔면을 한 개씩 더 먹을 때 만족의 누적은 조금씩 늘어나지만, 상대적 만족감은 줄어드는 것을 표현한 것이다. 이를 달리 말하면 비빔면의 총효용은 증가하지만 한계효용은 점차 감소한다고 할 수 있다.

이런 한계효용개념의 도입으로 인간의 경제활동에서 얻는 만족도를 수치로 표현할 수 있게 됐다. 우리가 덥거나, 차가운 느낌을 온도라는 수치로 표현하는 것처럼 우리가 어떤 물건을 소비할 때 얻는 만족도를 객관적 수치로 표현할 수 있게 된 것이다.
 

뷔페를 제대로 즐기는 방법은?

한계효용 체감의 법칙을 쉽게 찾을 수 있는 곳이 뷔페다. 뷔페는 평소에 접하지 못했던 음식을 다양하게 먹을 수 있어 많은 사람들이 찾는다. 많이 먹기 위해 끼니를 거르고 가지만, 몇 접시 먹지 못하고 안타깝게 뷔페를 나선 경험이 있을 것이다. 어느 정도 먹은 이후에는 한 접시를 더 먹을수록 만족감이 떨어져 더 이상 먹을 수 없기 때문이다.

그렇다면 뷔페에서 어떻게 먹어야 가장 큰 만족감을 얻을 수 있을까? ‘한계효용 균등의 법칙’에서 답을 찾을 수 있다. 각 상품의 1원어치 한계효용이 똑같을 때는 주어진 소득으로 한 상품을 덜 소비하고 다른 상품을 더 소비해도 총 효용이 더 이상 증가되지 않는다. 이런 때 소비자는 최대의 효용을 얻게 되는데, 이를 가리켜 한계효용균등의 법칙이라고 한다.

잠시 뷔페 식당에서 떠나 편의점으로 옮겨 삼각김밥과 우유를 먹는다고 가정해 보자. 이때 삼각김밥의 가격은 800원, 한계효용은 1600이다. 한편 음료수의 가격은 600원이고, 한계효용은 900이다. 삼각김밥과 우유의 1원당 한계효용은 각각 , 이다. 즉 1원당 한계효용은 삼각김밥이 크므로, 이때는 삼각김밥을 먹어야 한다.

하지만 삼각김밥을 더 먹을수록 한계효용은 점점 작아지게 돼, 결국 우유의 한계효용보다 작아지게 된다. 이때는 우유를 먹어 총효용을 높일 수 있다. 더 나아가 1원당 한계효용이 같아질 때까지 먹으면 가장 큰 효용을 얻을 수 있다.

뷔페에서도 자신이 가장 좋아하는 한 가지 음식만 먹는 것이 아니라 다양한 음식을 조금씩 먹어야 만족도가 극대화된다. 아무리 초밥을 좋아한다고 해도 계속 먹으면 한계효용(하나를 더 먹을 때 마다 생기는 만족도)이 줄어들고(한계효용 체감), 결국 다른 음식이 주는 효용(만족도)보다 작아지는 상태가 된다. 이때부터 다른 음식을 먹기 시작하면, 이 음식의 효용이 초밥의 효용보다 커 더 많이 먹을 수 있다. 이렇게 여러 가지 음식을 조금씩 먹어 보는 것이 가장 ‘수학적이고, 경제학적인 식사’다.

돈이 많으면 많을수록 더 좋을까?

그런데 돈도 한계효용 체감의 법칙을 따를까? 18세기의 수학자 다니엘 베르누이는 이 문제에 대한 답을 제시하기 위해 다음과 같은 문제를 냈다.

동전을 던져 앞면이 나오는 한 계속해서 던질 수 있다. 이때 참가자에게 주어지는 상금은 2ⁿ원이다. 그러나 언제든 뒷면이 나오면 경기가 끝난다. 즉 참가자가 처음 동전을 던졌을 때 뒷면이 나오면 상금은 없고 경기가 끝난다. 그러나 동전을 던져 한 번 앞면이 나온 다음 뒷면이 나오면 2원을 상금으로 받는다. 또 세 번 앞면이 나오고 그 다음에 뒷면이 나오면 상금은 8원이 된다. 하지만 만일 30번을 연이어서 앞면이 나오면 상금은 무려 약 11억 원이 된다. 이런 조건에서 이 경기에 참가하기 위해 얼마의 참가비를 내겠는가?

이 문제에서 한 번 던질 때의 기댓값(상금×확률)은 언제나 1원이다. 따라서 만일 동전을 다섯 번까지 던질 수 있다고 하면 기댓값은 5원이 된다. 이 문제에서는 동전을 무한히 던질 수 있으므로, 전체 기댓값은 무한대다. 그런데 이 문제를 실제로 사람들에게 내면, 대부분 이 내기에 1원보다 작은 돈을 내더라도 참가하려고 하지 않는다.

이렇게 기댓값이 무한해도 사람들이 참가하지 않는 것을 두고 다니엘은 기댓값이 단순한 금액이 아닌 한계효용의 합, 즉 총효용이어야 한다고 주장했다. 또한 “부의 증가로 발생하는 효용은 그가 이미 갖고 있는 돈의 양에 반비례한다”며, “같은 기댓값을 갖는다 하더라도 일어날 확률이 적을 경우 효용은 그 확률에 비례해서 작아진다”고 말했다.

두 번째 동전 던지기에서 상금 4원의 가치는 첫 번째 동전 던지기에서의 2원 가치의 두 배에 못 미치며, 세 번째 동전 던지기에서 받을 수 있는 8원의 가치는 두 번째 동전 던지기에서 받을 수 있는 4원 가치의 두 배가 안 된다는 것이다. 즉 가능성이 적고 실현 값이 큰 확률 사건의 실제 효용은 그 사건의 기댓값보다 월등히 작다는 논리다.

이는 돈도 한계효용 체감의 법칙을 따른다는 것을 보여주는 예이다. 1만 원을 가졌을 때 1만 원을 더 갖는 만족감과 1억 원을 가졌을 때 1만원을 더 갖는 만족감 중, 당연히 앞의 경우가 더 만족감이 크다.

뷔페에서부터 화폐까지 경제활동을 하며 느끼는 인간의 만족감을 수치로 표현한 것을 경제학에서는 ‘한계혁명’이라고 부른다. 이 한계혁명은 경제학에 큰 변화를 가져왔다. 이에 따라 모든 상품의 수요를 가격이나 소비자의 소득, 선호에 따라 함수로 표현할 수 있게 됐고 마찬가지로 공급도 공급함수로 나타날 수 있게 됐다. 즉 인간의 모든 경제활동을 수학적으로 표현할 수 있게 된 것이다.