d라이브러리

조합론의 고전 문제, 그래프 색칠하기

본격적으로 허 교수가 해결한 주요한 문제들을 살펴봅시다. 조합론의 고전적인 문제로 ‘4색 정리’가 있습니다. 평면지도에 있는 모든 나라를 4가지 색만 써서 구분해 색칠할 수 있는지 묻는 것입니다. 1852년 영국의 대학생이던 프랜시스 구드리가 지도를 관찰하다 처음 발견했고, 이를 은사이자 당대 저명한 수학자인 오거스터스 드 모르간에게 물으면서 수학자들의 관심을 끌게 됐습니다. 100년 넘게 많은 수학자의 노력이 지속적으로 이어졌고, 1976년 미국 일리노이대학교의 두 교수 케네스 아펠과 볼프강 하켄이 컴퓨터의 도움을 받아 증명을 완성했습니다.

쾨니히스베르크의 다리 문제처럼 이 지도 문제도 그래프로 바꿔 생각하는 것이 편리한데요. 각 나라를 점으로 표현하고, 두 나라가 인접하면 변으로 연결해 지도마다 그래프 하나를 얻습니다.

4색 정리에 자극을 받아 1932년 조지 벌코프와 해슬러 휘트니는 ‘채색 다항식’이라는 함수를 정의합니다. 채색 다항식이란 어떤 그래프에서 이웃한 꼭짓점은 서로 다른 색이 되도록 꼭짓점을 q개 이하의 색으로 칠하는 방법의 수를 나타낸 식입니다.

예를 들어 다음과 같은 사각형 그래프 G를 하나 생각해 봅시다. 3가지 색을 써서 칠한다면 어떨까요? 꼭짓점 하나의 색을 정하고 나면 인접한 두 꼭짓점의 색이 같은 경우는 3×2×2=12 가지예요. 다른 경우는 3×2=6가지의 방법이 있으므로 18가지입니다. 이처럼 계속 구해 보면 그래프 G의 채색 다항식은 χ_G(q)  = q⁴ - 4q³ + 6q² - 3q임을 확인할 수 있습니다.

색이 3가지일 때를 두 가지 경우로 나눠 구했는데, 이를 일반화 하면 ‘제거-축약 공식’을 얻습니다. 임의의 변 e를 고르고, e의 두 꼭짓점을 v₁, v₂라고 합시다. 변 e를 제거한 그래프를 G₁이라 하고, 다시 G₁에서 꼭짓점 v₁과 v₂를 겹쳐 얻는 그래프를 G₂라고 합시다. 구하고자 하는 그래프 G의 채색 다항식은 G₁의 채색 다항식에서 G₂의 채색 다항식을 뺀 값입니다. 즉 χ_G(q) = χ_G1(q) - χ_G2(q） 입니다. 왜냐면 G₁의 채색 다항식은 v₁과 v₂가 서로 다른 색일 필요 없이 색칠하는 방법의 수이고, G₂의 채색 다항식은 v₁과 v₂가 같은 색으로 칠해지는 방법의 수이기 때문이지요.

허 교수의 첫 조합론 연구, 리드-호가의 추측

구체적인 그래프에 대해 채색 다항식을 많이 계산해 보면 흥미로운 패턴을 관찰하게 되는데, 식을 다음 꼴로 썼을 때 계수들이 증가하다가 어느 지점부터 감소하는 패턴을 보입니다.

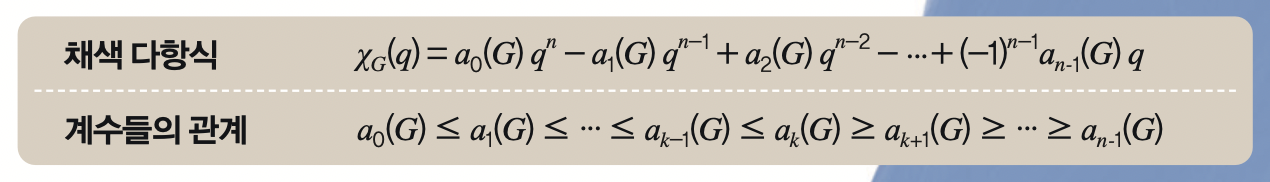
이런 패턴의 발현이 모든 그래프에 대해 참이라는 것이 ‘리드의 추측’입니다. 1968년 영국 수학자 로널드 리드가 제기한 추측으로, 채색 다항식의 계수를 앞에서부터 차례로 따져 봤을 때 증가하다가 감소한다는 것입니다.

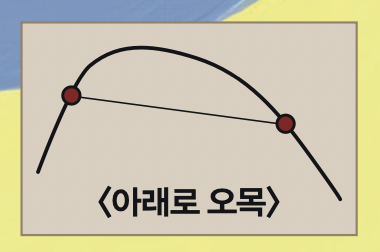
이 추측은 1974년 스튜어트 호가가 제기한 추측으로 강화됐는데, 계수들의 로그 값이 아래로 오목한 ‘로그-오목’이라는 것입니다. 곡선 위에 임의의 두 점을 잡아 직선으로 연결했을 때 그 직선이 곡선보다 아래에 있으면 아래로 오목하다고 합니다. 이 곡선에 로그를 취하면 더 완만한 곡선이 그려지는데, 이것이 로그-오목입니다. 로그-오목이면 항상 증가하다 감소합니다.