d라이브러리

뽀뽀를 부르는 수일까? 입맞춤 수

‘입맞춤 수’라는 이름만 들으면 뽀뽀의 횟수나 사랑에 관한 수일 것 같아 호기심이 생긴다. 하지만 실상은 몇백 년 동안 수학자가 연구한 난제와 관련이 깊다. 관련 연구로 필즈상을 받은 수학자도 있다.

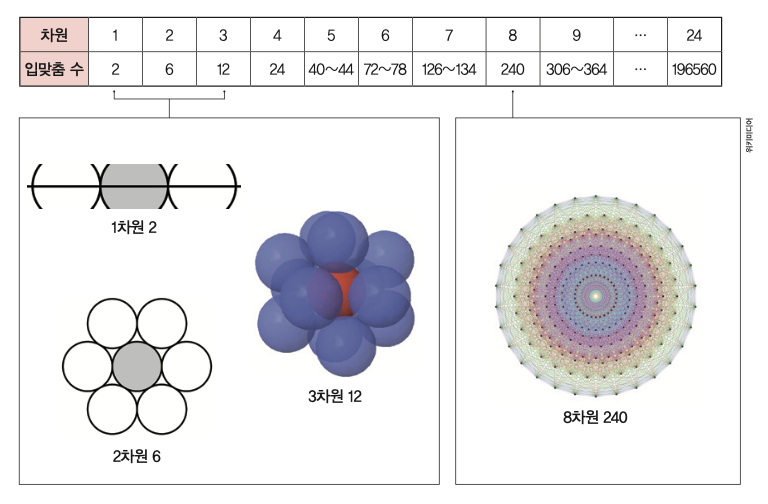
수학자들은 각 차원에서 반지름의 길이가 1cm인 단위 구를 중심으로 서로 겹치지 않게 단위 구를 최대 몇 개까지 접하게 놓을 수 있는지 연구했다. 그런데 단위 구가 서로 맞닿아 있는 모습이 단위 구끼리 뽀뽀하는 것처럼 보여 이 문제를 ‘입맞춤 수 문제’라고 이름 붙였다. 각 차원에서 구해지는 최대 단위 구의 개수는 입맞춤 수라고 한다. 

입맞춤 수는 1차원에서 2, 2차원에서 6이다. 3차원에서는 12인데, 그 증명은 매우 까다롭다. 17세기 영국의 물리학자이자 수학자인 아이작 뉴턴은 12, 스코틀랜드의 수학자 데이비드 그레고리는 13이라고 주장했다. 둘은 끝내 정확한 답을 내지 못했고, 이 연구는 20세기까지 이어졌다. 그러던 1953년 네덜란드의 수학자 바르털 판데르바르던과 독일의 수학자 구르트 슈테가 3차원 입맞춤 수는 12라고 증명해 문제를 해결했다. 

4차원에서 입맞춤 수는 오랫동안 24 또는 25라고 알려져 있었다. 그러다 1993년 미국의 수학자 존 콘웨이와 영국의 수학자 닐 슬론이 24라고 증명했다. 5차원 이상에서는 8차원과 24차원의 입맞춤 수만 정확히 알려져 있다. 각각 240과 19만 6560이다.

케플러 추측의 해답으로 입맞춤 수 구한다!

입맞춤 수를 찾는 문제는 수학계 유명한 난제인 ‘케플러 추측’과도 관련이 깊다. 공간에서 단위 구를 겹치지 않으면서도 가장 밀집하게 배치하는 방법을 찾는 것이 케플러 추측인데, 2차원과 3차원, 8차원, 24차원에서는 그 방법대로 단위 구를 놓으면 자연스럽게 입맞춤 수를 구할 수 있기 때문이다. 

예를 들어 2차원 입맞춤 수는 단위 원(2차원의 단위 구)을 중심에 두고 정육각형 형태로 단위 원을 배열했을 때 구해지는데, 2차원 케플러 추측의 답이 이 형태로 단위 원을 놓는 것이다. 왜 그런지 자세히 들여다보자. 

평면에 단위 원을 조밀하게 배치하는 방법은 크게 두 가지다. 하나는 정사각형 격자의 꼭짓점에 원의 중심을 배치하는 것, 다른 하나는 정육각형 격자의 꼭짓점에 원의 중심을 배치하는 것이다. 정사각형과 정육각형 모두 각 도형을 연달아 이어붙이면 평면을 빈틈없이 메울 수 있으니 그 구조로 원을 배치하고, 버려지는 공간이 얼마나 되는지 따져보자. 즉 원의 지름과 정사각형, 정육각형의 한 변의 길이가 a라고 할 때 원이 덮는 넓이의 비율을 구해보자. 

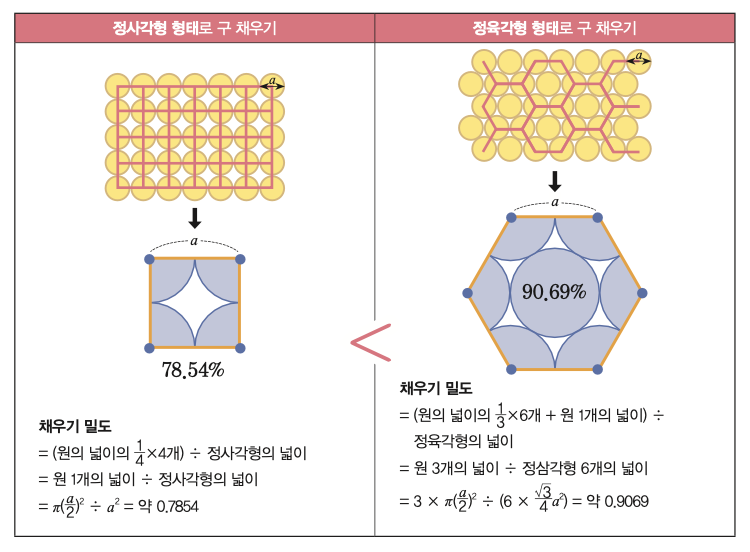
이처럼 단위 원을 정육각형 형태로 배열했을 때 밀집도가 더 높다. 이때 입맞춤 수가 6이다.

8차원, 24차원 케플러 추측 해결해 2022 필즈상 수상

3차원에서는 상하좌우 어느 방향에서 봐도 정육각형 형태를 이루는 ‘면심 입방 격자’ 위에 단위 구를 빽빽하게 놓는 것이 케플러 추측의 해답인데, 이렇게 단위 구를 놓으면 3차원 입맞춤 수인 12를 구할 수 있다. 8차원과 24차원에서도 마찬가지로 케플러 추측의 해답으로 단위 구를 배치하면 입맞춤 수를 알 수 있다. 

케플러 추측은 1600년대 초 독일 천문학자 요하네스 케플러에 의해 연구가 시작됐다. 그는 ‘육각형 눈송이에 관한 글’에서 3차원 공간에서 단위 구를 가장 밀도 높게 쌓는 방법을 제안했다. 과일가게에서는 사과나 귤과 같은 둥근 모양의 과일을 피라미드 형태로 쌓는데, 그렇게 쌓았을 때 밀도가 가장 높다고 추측한 것이다. 

케플러의 이런 추측을 수학적으로 증명하기까지 꽤 오랜 시간이 걸렸다. 2차원 문제는 1940년대 헝가리 수학자 라슬로 페예시 토트가, 3차원 문제는 미국 수학자 토마스 헤일스가 1998년에 해결했다. 

2015년까지 4차원 이상의 문제에 관해선 해결된 게 없었다. 우크라이나-스위스 수학자 마리나 비아조프스카가 8차원에서는 ‘E8 격자’로 불리는 특수한 격자 위에 단위 구를 놓으면 최적이라고 연구해 논문을 발표했다. 이를 본 수학자들이 24차원에서도 8차원 해결법이 통할 것 같다고 제안했고, 일주일 만에 24차원에서는 ‘리치 격자’ 위에 단위 구를 배치하면 최적이라고 증명했다. 비아조프스카는 이 연구 업적을 인정받아 2022년 필즈상을 거머쥐었다. 

필즈상은 수학에서 탁원한 업적을 세운 만 40세 이하 젊은 수학자에게 주는 수학계 최고 권위 학술상이다. 4년마다 열리는 세계수학자대회에서 최대 4명까지 상을 준다.