d라이브러리

램지 수가 변을 두 가지 색으로 칠하는 그래프 문제라면, 세 가지 이상의 색으로 칠하는 문제도 있습니다. 이를 ‘다색 램지 수’라고 부릅니다. 두 가지 색을 칠하는 기본 램지 수 문제는 앞서 소개한 것처럼 서로 알거나 모르는 경우로 생각할 수 있습니다. 그럼 세 가지 색을 칠하는 다색 램지 수는 어떤 상황에 비유할 수 있을까요? 램지 수를 연구하는 이준경 영국 런던대학교 수학과 박사후연구원은 동네 친구 모임에서 ‘동창이 아닌 경우’, ‘동창은 맞지만 같은 반인 적이 없는 경우’, ‘동창이면서 같은 반인 적이 있는 경우’에 비유할 수 있다고 말했습니다.

다색 램지 수의 가장 간단한 경우인 R(3,3,3)≤17을 증명해 보겠습니다. 이를 위해서는 꼭짓점이 17개인 완전그래프의 각 변에 세 가지 색을 어떻게 칠해도 한 가지 색으로 이뤄진 삼각형이 만들어짐을 보여야 합니다.

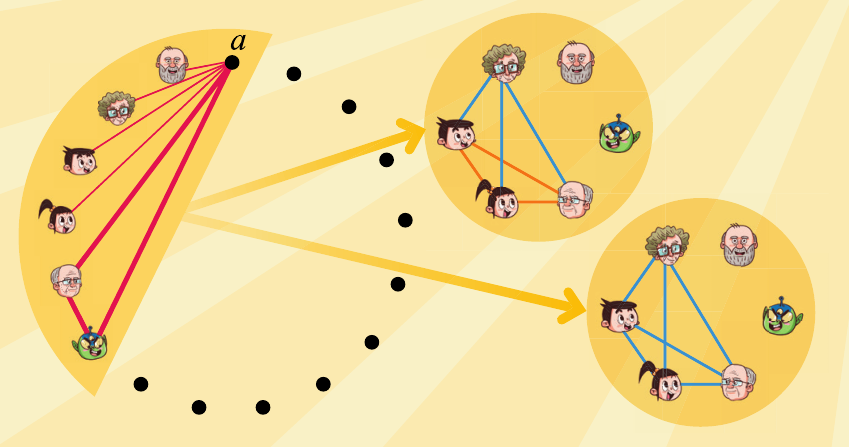
꼭짓점이 17개인 완전그래프의 각 변을 빨강, 파랑, 주황 3가지 색으로 칠한다고 가정하겠습니다. 한 점 a에서는 16개의 변을 그을 수 있습니다. 앞서 R(3,3)을 칠한 방식과 같이, 빨강을 먼저 칠할 때 한 점 a와 연결된 16개의 변 중 6개는 빨강으로 칠해야 합니다. 5개씩 빨강, 파랑, 주황을 칠할 때 남는 한 변은 꼭 빨강, 파랑, 주황 중 하나로 칠해야 하니까요. 다른 색으로 먼저 칠한다면 그 색이 6개가 될 수 있겠죠.

점 a와 빨강으로 이어진 6개의 점 중 2개를 골라 빨간 선으로 이으면 아래의 그림처럼 빨간 삼각형이 만들어지기 때문에 a와 빨강으로 이어진 점들 사이는 파랑과 주황으로만 칠해야 합니다. 그런데 R(3,3)=6에서 확인한 것처럼 빨강으로 이어진 6개 점 사이를 파랑과 주황으로 칠한다면 파란 삼각형이나 주황 삼각형이 반드시 존재하게 됩니다. 따라서 R(3,3,3)≤17임을 알 수 있습니다.

그래프에 확률까지 도입한 에르되시

그렇다면 크기가 매우 큰 완전그래프를 여러 색으로 칠할 때 한 가지 색으로 둘러싸인 부분 완전그래프가 생기지 않도록 해야 한다면 여러분은 어떤 방법으로 칠할 건가요? 만약 빨강, 파랑, 주황 세 가지 색을 이용해 칠한다면 가장 먼저 빨간 삼각형이 생기지 않도록 칠하고, 그런 다음 파란 삼각형이 생기지 않도록 칠하려고 할 겁니다. 

하지만 빨간 삼각형이 생기지 않도록 칠하려다 보면 이내 파란 삼각형이 생기고, 파란 삼각형이 생기지 않도록 칠해 보면 주황 삼각형이 생겨 원하는 결과를 얻기 어렵다는 걸 알게 됩니다. 열심히 머리를 써서 칠해도 원하는 결과가 안 나오다 보니 에르되시는 다른 방식으로 접근하기로 합니다. 각 변을 무작위로 칠할 때 한 가지 색으로 이뤄진 부분 완전그래프가 생기지 않을 확률이 얼마인지 계산하는 것입니다. 이를 ‘확률적 방법론’이라고 부릅니다. 계산한 확률이 0보다 크면 부분 완전그래프가 없도록 칠할 수 있다는 뜻입니다. 구체적인 예를 구하지 않아도 부분 완전그래프가 존재한다는 것을 알 수 있어 모든 경우의 수를 따져 구하는 방식에 비해 훨씬 효과적입니다. 이 방법으로 에르되시는 램지 수가 존재할 범위의 최솟값인 하한을 구했습니다.