d라이브러리

삼각형은 변의 수가 가장 적은 다각형으로 모든 도형의 기본이다. 삼각형 자체를 중심분할해 작은 삼각형 3개로 나눌 수 있고, 사각형에 대각선을 그어서 삼각형 2개 또는 4개로 만들 수도 있다. 마찬가지로 오각형도 삼각형 3개 또는 5개로 나눌 수 있다. 이처럼 어떤 다각형도 여러 개의 삼각형으로 나눌 수 있으며, 비슷한 방법으로 다면체인 입체도형도 여러 개의 삼각형의 결합으로 나타낼 수 있다.

이런 원리를 이용해 도형을 견고하게 분할하는 방법이 있다. ‘들로네 삼각분할’이다. 들로네 삼각분할은 평면 위의 점을 연결해 삼각형을 만들어 공간을 분할하는 방법이다. 각 삼각형은 최대한 정삼각형에 가까워야 한다. 이 삼각형은 어디에 이용될 수 있을까?

도시와 도시를 연결하는 도로망을 설계할 때 이 들로네 삼각분할을 참고 모형으로 활용한다. 한 도시에서 다른 도시로 이동할 때, 두 도시를 연결하는 도로가 없다면 다른 도시를 우회해 이동해야 한다. 이때 우회도로는 두 도시의 직선거리에 가능한 가까워야 한다. 들로네 삼각분할을 이용해 도로를 연결하면 우회도로의 이동거리를 어느 정도 짧게 만들 수 있다. 또한 들로네 삼각분할은 컴퓨터 그래픽 분야에서 모델링이나 3D애니메이션으로 3D입체를 만들 때도 유용하게 쓰인다.

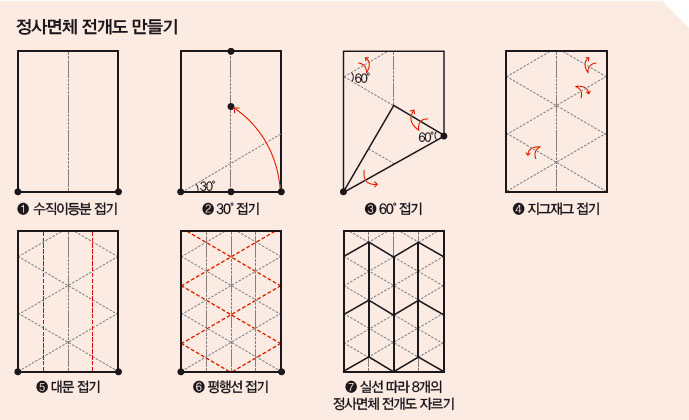
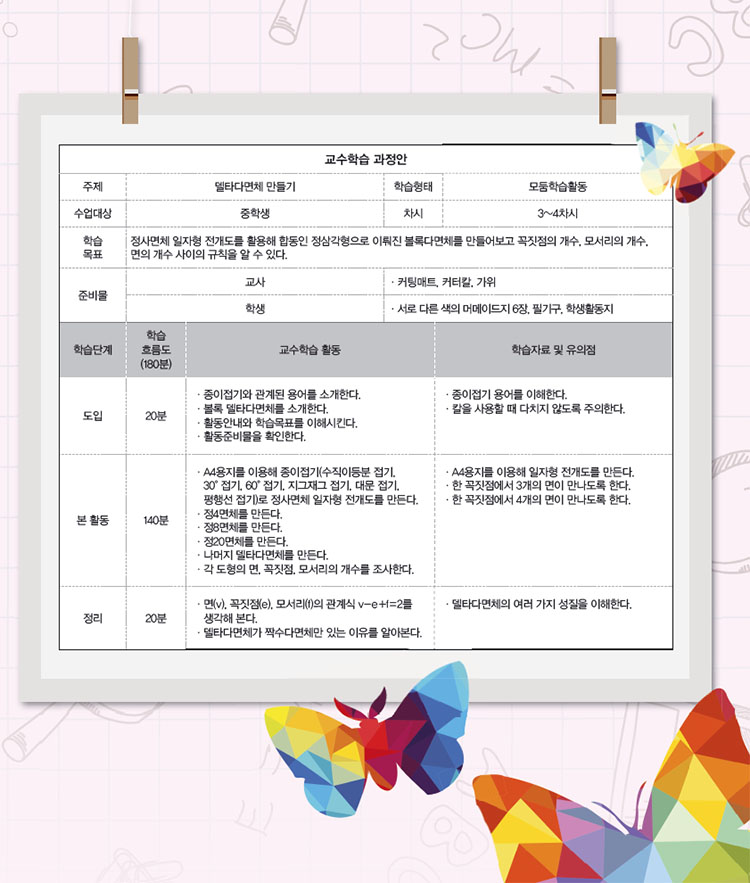
들로네 삼각분할과 다르게 모든 면이 서로 합동인 정삼각형으로 이뤄져야 하는 다면체도 있다. 바로 ‘델타다면체’다. 델타다면체는 모든 면이 정삼각형이어야 하지만, 각 꼭짓점에 모인 면의 개수는 달라도 되는 볼록다면체다. 여러 모양의 델타다면체를 만들어보며 삼각형 세계의 더 깊숙한 곳으로 빠져보자!