d라이브러리

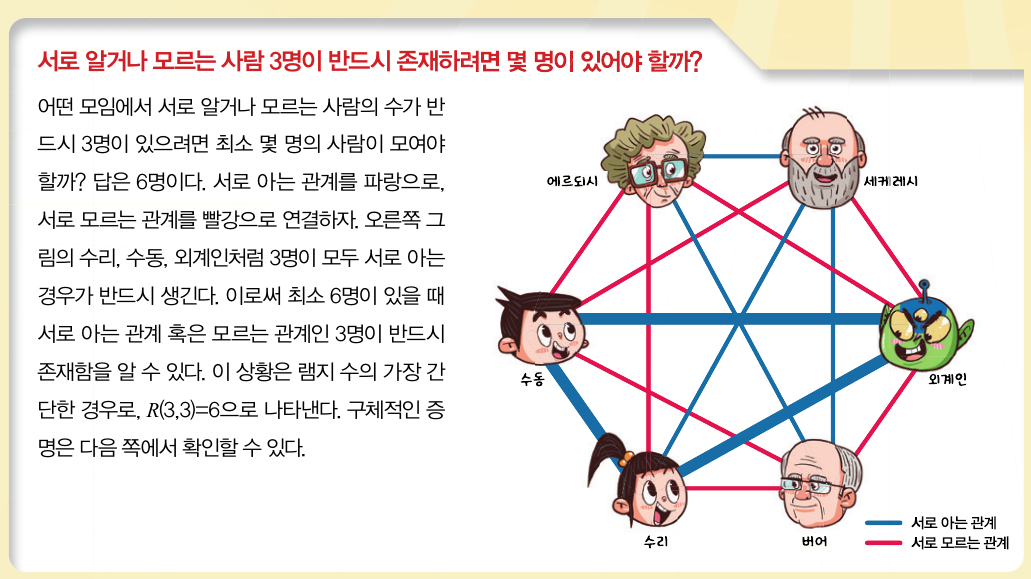
완벽한 혼돈은 가능할까요? 크고 무질서한 구조 속에서 작은 조화로운 부분을 항상 찾을 수 있는지 연구하는 분야를 ‘램지 이론’이라고 합니다. 1928년 영국의 수학자 프랭크 램지는 사람이 충분히 많다면 그중 서로 모두 아는 관계인 r명 혹은 서로 전혀 모르는 관계인 s명이 반드시 있다는 ‘램지 정리’를 발표했습니다. 이때 A와 B가 아는 사람이려면 A가 B를 알면서 B도 A를 알아야 합니다. 이를 만족하는 최소의 정수 N을 ‘램지 수’라 부르며, R(r,s)=N으로 나타내죠. 즉, 램지 수는 서로 알거나 모르는 사람의 수 r 또는 s를 존재하게 하는 최소의 전체 인원이라고 할 수 있습니다. 램지 수는 1947년 헝가리의 수학자 에르되시 팔과 세케레시 죄르지가 제시했어요.

램지 수의 정확한 값을 구하기는 매우 어렵습니다. r과 s의 값이 늘어날수록 고려해야 할 경우의 수가 기하급수적으로 커지기 때문입니다. 가장 간단한 램지 수인 R(3,3)을 모든 경우의 수를 따져 구하려면 2¹⁵가지, 즉 3만 2768번을 다 따져봐야 합니다. 서로 알거나 모르는 사람의 수가 10명일 때는 고려해야 할 경우의 수가 수백억 가지로 늘어납니다.

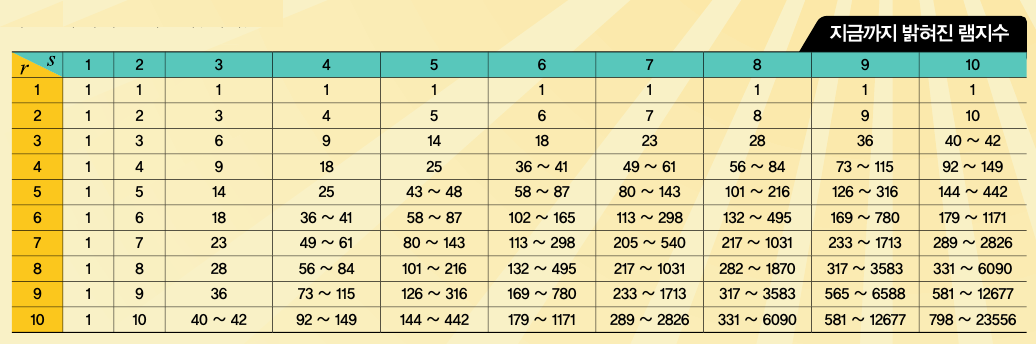
가능한 모든 경우의 수를 따져 구하는 방식은 r과 s가 커지면 그 어떤 성능 좋은 컴퓨터를 사용해도 해결하기 어렵습니다. 이에 수학자들은 구체적인 램지 수를 구하는 대신에 램지 수가 존재하는 범위를 좁히는 방식으로 접근했습니다. 구하려는 램지 수의 범위에서 작은 쪽 경곗값인 ‘하한’을 높이고, 높은 쪽 경곗값인 ‘상한’을 낮추면 정확한 램지 수에 좀 더 가까워지기 때문입니다. 예를 들어 R(3,3)=6이라는 것은 R(3,3)이 6보다 작거나 같고 5보다는 크다는 연구 결과를 종합해 얻을 수 있었습니다. 또한 수학자들은 R(t,t)처럼 r과 s가 같은 경우로 좁히거나, R(3,t)와 같이 두 변수 중 하나를 고정해 램지 수를 구했습니다. 많은 수학자의 노력으로 지금까지 밝혀진 램지 수는 아래의 표와 같습니다.