d라이브러리

2001년 9월 4일, 네덜란드 헤이그에 있는 율리아나 아동 병원에서 암버르 자위데르베이크가 사망했어요. 의사들은 아이가 자연사했다고 판정했죠. 그런데 다음날, 병원은 의견을 번복하고 이렇게 발표했어요. “암버르가 살해당했다.” 

범인으로 지목된 것은 암버르가 사망할 때 현장에 있던 간호사 중 한 명인 루시아 더베르크였어요. 더베르크가 의심을 받은 이유는 ‘우연이라고 보기에는 환자가 사망하는 현장에 너무 자주 있었다’는 병원 관계자의 증언 때문이었어요. 암버르의 사망 소식을 들은 동료 간호사는 우려했던 일이 일어났다며 더베르크가 사망 현장에 있던 빈도수가 다른 간호사에 비해 높다고 보고했어요. 파울 스미츠 병원장은 환자가 중태에 빠졌을 때 더베르크가 현장에 있었던 횟수를 계산했죠. 

그 결과 더베르크가 율리아나 아동 병원에 근무했던 9개월 동안 1029번의 간호사 근무조 교대가 있었고, 병원이 ‘비자연사’로 분류한 7건의 사고가 모두 더베르크가 근무한 142번 동안 일어났다는 걸 확인할 수 있었어요. 더베르크가 휴무였던 날은 사고가 0건이었죠. 스미츠 병원장은 이 자료를 경찰에 제출했고, 더베르크는 흉기도 동기도 밝혀지지 않았지만 13건의 살인과 4건의 살인 미수 혐의로 기소됐어요. 

근거 자료를 검증할 증인으로 재판부가 선택한 것은 법학과 교수였어요. 헹크 엘페르스 네덜란드 암스테르담 자유대학교 교수는 율리아나 아동 병원을 포함해 더베르크가 이전에 일했던 병원에서의 근무표와 의사들이 제공한 자료를 바탕으로 더베르크가 ‘그렇게 많은 자연사 현장에 우연히 있을 확률’을 계산했어요. 

결과는 ‘3억 4200만분의 1’이었어요. 환자의 사망이 자연적으로 발생했다고 보기에는 너무나 낮은 확률이었죠.

 수학적 오류  숫자보다 중요한 건 통계 분포!

그런데 이 사건의 확률 계산에는 심각한 오류가 있었어요. 오류를 밝힌 것은 통계학 전문가 리하르트 힐과 페테르 흐륀발트 네덜란드 레이덴주립대학교 교수였어요. 더베르크가 감옥에 있는 동안 여전히 더베르크의 무죄를 믿는 사람들이 진상을 밝히기 위해 사건을 쫓고 있었거든요.

엘페르스 교수의 계산 방법에는 여러 오류가 있었지만, 그중 가장 치명적이었던 것은 ‘p값을 곱한 것’이었어요. p값은 ‘피셔의 정확 검정’이라는 통계 검사 방법으로 얻어지는 값으로, 외부 영향이 전혀 없을 때 숫자의 조합으로 이뤄진 어떤 사건이 완전히 무작위로 일어날 확률값이에요. p는 0과 1 사이의 값이며, p가 0.01이면 해당 사건이 100번에 1번 일어날 수 있다는 뜻이에요. 

엘페르스 교수는 더베르크가 일했던 세 병원에서 각각 3개의 p값을 구한 뒤 이것을 곱해 3억 4200만분의 1을 얻었는데, 이 세 값은 서로 독립적인 사건이 아니므로 곱하면 안 돼요. 

만약 어떤 간호사가 한 병원에서 근무하는 동안 실수가 일어날 p값이 일 때 이 간호사가 2개 병원에서 일했다면 여전히 각각의 p값은 에 가까울 거예요. 같은 간호사니까요. 그런데 2개 병원에서 실수할 확률을 구한다고 ×로 계산하면 250번에 1번 정도 일어날 수 있었던 실수가 갑자기 6만 2500번에 1번 일어날 수 있는 일로 둔갑해요. 더베르크의 확률값 3억 4200만분의 1도 이런 오류에서 발생한 것이었죠.

다시 정확한 방법으로 계산하자 라는 새로운 p값이 구해졌어요. 여전히 작은 확률이지만 네덜란드 전체 간호사 25만 명 중 200명 정도에게 일어날 수 있는 일이라는 뜻이므로 그렇게 의심스러운 값은 아니에요. 

결국 2006년 10월 새로운 조사 위원이 꾸려졌고, 더베르크는 암버르가 사망한 지 약 18년 만에 최종 무죄 판결을 받았어요.

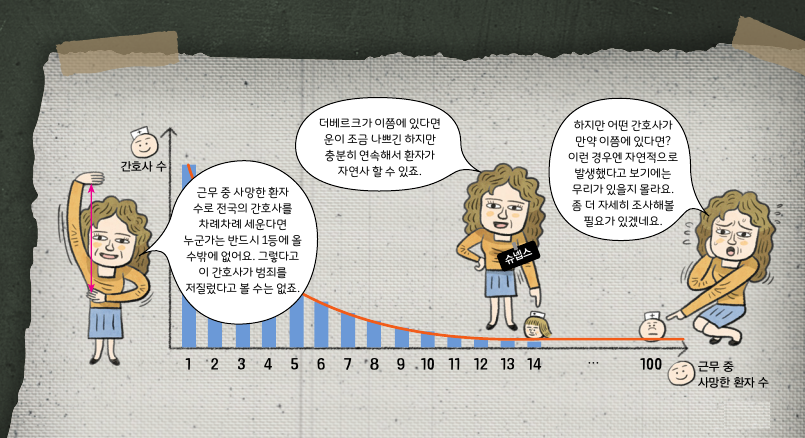
이처럼 확률값을 다룰 때 중요한 것은 단순한 숫자로 보는 것이 아니라 그 값이 사건이 일어날 수 있는 모든 경우를 그래프로 나타낸 통계 분포 안에 들어 있는지 아닌지를 판가름하는 거예요.